大規模言語モデル（LLM）は、Chain-of-Thought（CoT）プロンプティングを用いることで、数学的な問題解決から複雑な論理推論に至るまで、目覚ましい推論能力を発揮しています。しかし、推論過程を明示するCoTは、カスケードエラーという根本的な脆弱性を抱えています。これは、単一の誤ったステップが後続の結論全体を不正確または支離滅裂な出力にしてしまうためです。

従来の自己検証や自己改善フレームワークは、推論全体に対して大まかな評価を行う手法に頼っており、長い導出過程に埋め込まれた細かなステップごとの誤りを見つけ、正確に修正する能力に限界がありました。

この限界を克服するために提案されたのが、Socratic Self-Refine (SSR) という新しいフレームワークです。SSRは、LLMの推論プロセスを検証可能な「副次的な質問と回答のペア」（Socratic steps）へと再構築します。この分解により、ステップレベルでの精密な確信度推定と、エラー箇所を標的とした改善が実現し、より正確で解釈可能な推論連鎖の生成が可能になります。この記事では、このSSRの仕組みと優位性を詳しく解説していきます。

Socratic Self-Refine の基本概念

Socratic Self-Refine (SSR)の根底にあるのは、大規模言語モデル（LLM）による自然言語の推論過程が、目標設定と問題解決のステップのシーケンスとして暗黙的にモデル化されている という洞察です。SSRは、この暗黙的なプロセスを、一連の独立し、かつ検証可能な「副質問と副回答のペア」である Socratic Steps（ソクラテス的ステップ、あるいは対話的ステップ）と定義しています。

従来のChain-of-Thought (CoT)による推論トレースが連続した自然言語の記述であったのに対し、SSRはこの連なりを、対話のように構造化することで、推論の過程をより粒度の細かいモデリングへと昇華させます。

この分解プロセスは、特別な訓練を必要とせず、LLM自身がゼロショットプロンプトを用いて実行します。情報抽出や要約の技術を活用することで、既存の推論を Socratic Steps のシーケンスとして信頼性高く出力でき、推論過程を制御可能な構造としてモデル化します。

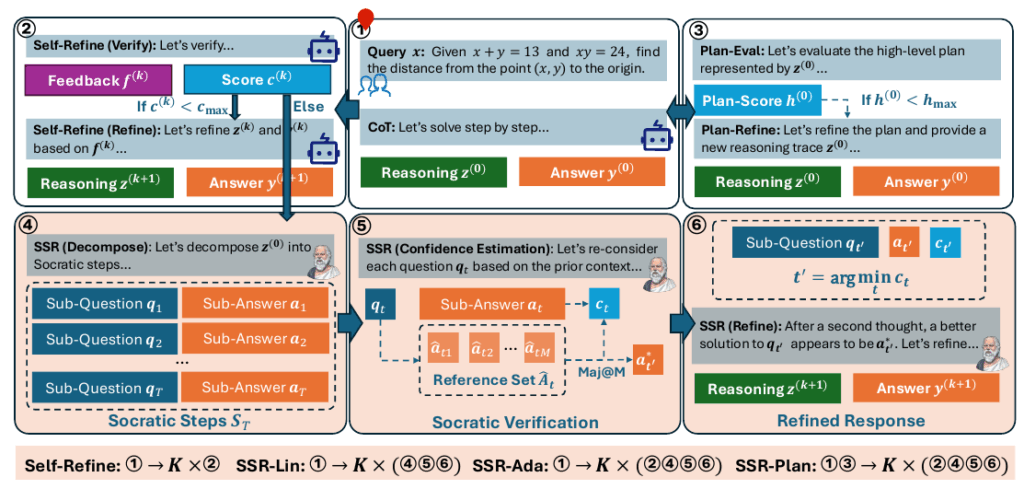
さらに重要な点として、この構造化は、各ステップにおける「計画」（次の質問の定式化）と「実行」（質問に対する回答の生成）を明確に区別します。従来の検証手法が、最終結果や全体的なロジックという「粗い粒度」に留まっていたのに対し、SSRはこの対話的構造を利用することで、推論のどのステップでどのような誤りが生じたのかを特定できる、「プロセスレベルでの精密な介入」を可能にします。

信頼性の定量化

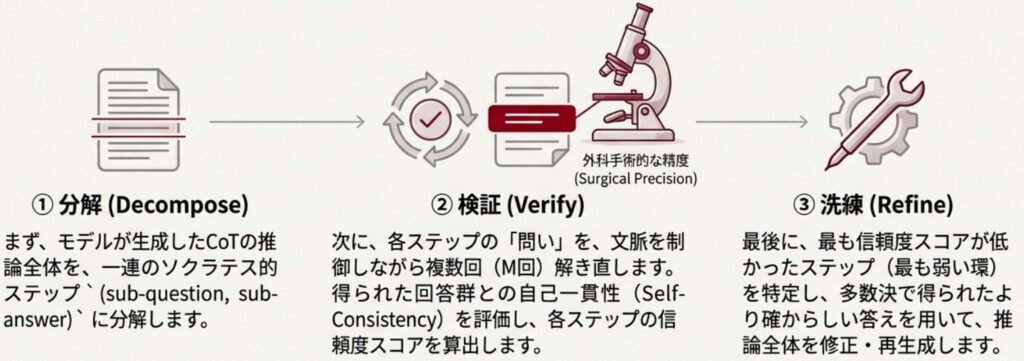
Socratic Self-Refine (SSR)の核となるのは、各 Socratic Steps の信頼性を正確に定量化する自己検証のプロセスです。従来の自己検証フレームワークが推論全体に自信度を付与するのに対し、SSRではこの検証をステップレベルで実行します。

このステップレベルの確信度推定を可能にするために、SSRは制御された再解決（Controlled Re-solving）という手法を採用します。具体的には、推論連鎖から分解された特定の副質問（\(q_t\)）に対し、LLMは以前のステップ（コンテキスト）の情報のみを用いて、その副質問を独立して\(M\)回再実行するよう促されます。

これにより、複数の異なる副回答（\(\hat{a}_{ti}\)）からなる 参照セット（Reference Set, \(\hat{\mathbf{A}}_t\)）が生成されます。

次に、元の推論ステップで生成された副回答（\(a_t\)）が、この参照セット\(\hat{\mathbf{A}}_t\)内でどれだけ一貫しているか（つまり、多数決によってどれだけ支持されているか）が比較されます。この比較に基づき、各ステップの確信度スコア（\(c_t\)）が推定されます。この手法は、複数のサンプル間の一致度を信頼性の指標とする自己一貫性チェック（Self-Consistency Checks）の原理を利用したものです。

このアプローチは、従来のフレームワークが依存していた曖昧な「フィードバック」ではなく、データに基づいた信頼性の定量化を可能にします。確信度スコアが低いステップを特定することで、特に数学などの厳密なタスクにおいて、推論連鎖の中で誤りが発生しやすい箇所をピンポイントで特定することが可能となり、LLMの内部的な推論プロセスを評価・解釈するための先駆的な取り組みとなります。

実践的な改善戦略

前セクションでステップごとの確信度スコア（\(c_t\)）について説明しましたが、Socratic Self-Refine (SSR) で特に重要となるのは、この定量的な情報に基づき、推論を効率的かつ正確に修正する戦略です。

エラーの特定と標的型修正

SSRはまず、推論連鎖全体の中で最も確信度の低いステップ（\(t’\)）を特定します。これは \(t’ = \mathrm{arg} \hspace{1mm} \mathrm{min}_{t} \{c_t\}_{t \in [T]}\) という形で計算されます。このステップ \(t’\) が、推論の連鎖的な誤りの発生源として、最も修正が必要な箇所であると判断します。

次に、この特定された「最も弱いステップ」の修正に取り組みます。ステップ \(t’\) の副質問（\(q_{t’}\)）に対して、参照セット（Reference Set, \(\hat{\mathbf{A}}_{t’}\)）を活用し、多数決を適用します。これにより、最も一貫性の高い、つまり統計的に最適化された副回答 \(\mathbf{a}_{t’}^{*}\) が導出されます。

この最適化された回答 \(\mathbf{a}_{t’}^{*}\) は、元のステップの質問 \(q_{t’}\) と元の回答 \(a_{t’}\) と共に Socratic Feedback として構成され、LLMに注入されます。

効率的な局所的修正

従来の自己洗練（Self-Refine）が推論全体に対する大まかなフィードバックに頼っていたのに対し、SSRはこのターゲットを絞った局所的な修正を実施します。

LLMは、この精密なフィードバックを受け取ることで、推論全体を最初からやり直すことなく、特定されたエラー（\(q_{t’}\) の回答）のみを効率的に修正し、新しい推論トレース \(\mathbf{z}^{(k+1)}\) を生成します。この「狙いを定めた修正」の繰り返しにより、推論の精度と解釈可能性を向上させ、CoT推論におけるカスケードエラーの発生を効果的に抑制します。

このアプローチは、LLMが学習時（Instruction TuningやPreference Tuning）に採用するChain-of-Thoughtのような構造を崩さないよう、フォーマットの混乱を最小限に抑えながら、必要な情報のみを自己洗練コンテキストに注入する設計原則に基づいています。

実装への応用

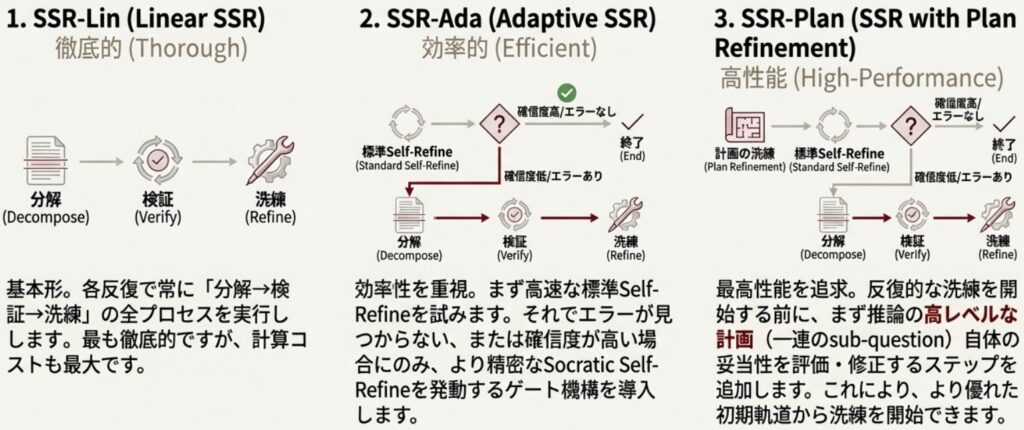
Socratic Self-Refine（SSR）のステップレベルの検証は非常に強力ですが、すべての反復ステップで実行すると、標準的なSelf-Refineフレームワークと比較して計算コストが大幅に高くなるという実務的な課題があります。このため、SSRは効率性とロバスト性を両立させるために、2つの主要な型を提供しています。

効率と堅牢性を両立する型

1. Adaptive SSR (SSR-Ada)： これは、効率性を重視したゲーティングメカニズムを採用しています。まず、安価な検証が可能な標準的なSelf-Refineを主要な洗練方法として適用します。Self-Refineが推論のエラーを検出できなかった場合、あるいはレスポンスがすでに正しいと判断され過度に自信を持っている場合など、追加の検証が必要な場合にのみ、コストの高いSSRが起動されます。これにより、オーバーヘッドを削減しつつ、詳細検証の余地を残すことが可能です。
2. SSR with Plan Refinement (SSR-Plan)： SSR-Planは、SSR-Adaに加えて、反復的なステップレベルの改善に入る前に、推論のハイレベルな計画の妥当性を一度評価し修正する初期プロセスを追加します。この計画の健全性を最初に確保することで、その後のステップレベルの修正効果が増幅され、より安定した結果が得られます。

技術的利点と実用例

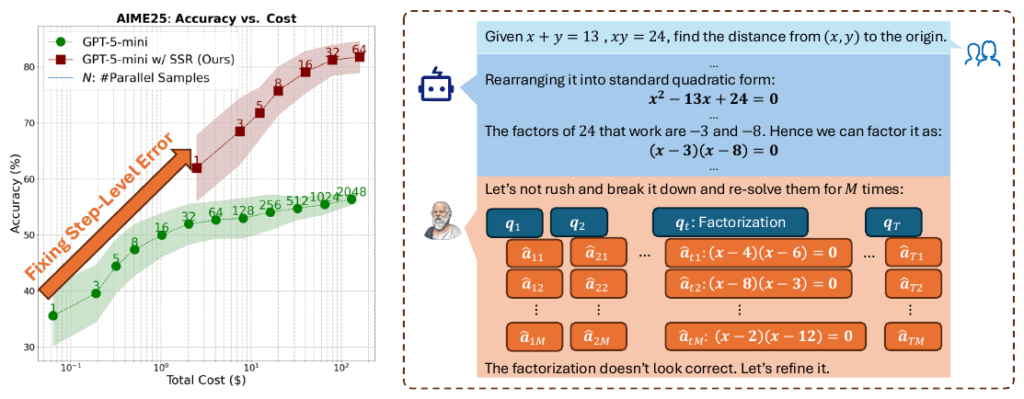
SSRは、既存の反復型改善手法を一貫して上回ります。特に数学的推論（AIME、MATH-Level-5）や論理的推論（Zebra Puzzle、Mini-Sudoku）といった多数の複雑な推論タスクにおいて優位性を示し、中でもSSR-Planは最もロバストな結果を達成しています。

• ロバスト性の確保: SSRは、モデルの能力に依存せず推論能力を向上させることが確認されています。特に挑戦的な問題（Humanity’s Last Exam, HLE）や、強力なモデル（GPT-5）においても、バニラなSelf-Refineが機能不全に陥り、性能が低下する場合がある中でも、SSRは着実に性能を向上させます。
• 実装ヒントと安定性: SSR-Planの採用は、単に性能を向上させるだけでなく、実装上のメリットもあります。Plan Refinementを追加することで、推論過程の分解におけるステップの粒度（Socratic Stepsの数）に対する性能の感度が低下し、実装の安定性が高まることが分析により示されています。

おわりに

Socratic Self-Refine (SSR) は、大規模言語モデル（LLM）の推論評価を、最終結果の抽象的な判断から、プロセスレベルの体系的な検証へと移行させる重要なパラダイムシフトをもたらしました。

推論過程を、検証可能な副質問と副回答のシーケンス、すなわちSocratic Stepsとして明示的にモデル化することで、モデルの「思考」をより透明化します。これにより、どこで、なぜ誤りが発生したかを正確に理解し、標的を絞った修正や制御可能な介入が可能となります。

SSRは、様々な複雑な推論タスクにおいて既存の反復型改善手法を一貫して上回る性能を示し、特に高精度な多段階論理が要求されるシステムにおいて、信頼性が高く、説明責任を果たせるLLMアプリケーションを構築するための強力な基盤を提供します。

SSRの導入は、LLMを単なる推論エンジンとしてではなく、推論過程の信頼性を確保できる、より信頼できるシステムへと進化させる重要な手法となり得ます。

More Information

• arXiv:2511.10621, Haizhou Shi et al., 「SSR: Socratic Self-Refine for Large Language Model Reasoning」, https://arxiv.org/abs/2511.10621