現代の宇宙物理学は、GaiaやDESI、LSSTといった大規模な天文サーベイによって、ビッグデータの時代へと突入しました。数十年前の観測が数千のソースを扱っていたのに対し、現在では数十億もの天体の観測データが日常的に生成されています。このような膨大なデータ量を効率的に処理するためには、スケーラビリティ（拡張性）に優れた新しいデータ解析手法が不可欠です。

しかし、古典的な統計的手法や機械学習のアプローチは、「スケーラビリティ」「表現力」「データ効率性」という3つの特性を同時に達成することが困難です。例えば、ガウス過程は表現力に優れますが、大規模データセットでは計算負荷が高くなりすぎます。

深層学習（Deep Learning）は、GPUによる並列計算を通じて高いスケーラビリティと、任意の連続関数を近似する強力な表現力を提供します（普遍近似定理）。さらに深層学習は、物理学の専門知識をモデルのアーキテクチャに組み込むことで、この課題を克服しつつあります。

基礎概念 — バイアスと次元の呪い

深層学習を単にデータからパターンを抽出する強力なツール、あるいは複雑な関数を近似する近似器（Universal Approximator）として捉えるだけでは、その真価を見誤ってしまいます。深層学習が現代宇宙物理学で成果を上げているのは、それが物理学的な専門知識や仮定をモデル構造に組み込むためのフレームワークとして機能する点にあるためです。

次元が増すことの代償 — 「次元の呪い」

古典的な統計的手法や機械学習手法が、スケーラビリティとデータ効率性のバランスを取るのが難しい根本的な理由の一つは、「次元の呪い（Curse of Dimensionality）」にあります。ここでいう次元とは、データセットの特徴量の数を指します。

次元数（\(d\)）が増加するにつれて、データ空間の体積は指数関数的に拡大するため、必要なデータ量も爆発的に増大します。その結果、高次元空間ではデータ点が互いに指数関数的に孤立し、「孤立した島」のようになってしまいます。

ランダムフォレスト（Random Forests）のような、隣接点に基づいて予測を行うアルゴリズムは、高次元空間では隣接するデータ点を見つけることが極めて稀になるため、トレーニングデータの範囲外にあるデータ（探索されていない領域）に対して外挿し、一般化することが原理的に不可能になります。古典的な手法は、この制限により、高次元空間でスケーラビリティ、表現力、データ効率性の3つの特性を同時に達成できません。

誘導バイアスの導入

深層学習がこの限界を克服し、限られたデータから効率的に一般化を可能にする鍵は、誘導バイアス（Inductive Bias）の導入です。誘導バイアスとは、学習アルゴリズムを数ある解の候補の中から特定の、より望ましい解に導くための、設計に組み込まれた前提や仮定のことです。

天文学者も、この誘導バイアスを日常的に活用しています。たとえば、銀河の輝度プロファイルやスペクトル線のモデル化において、物理的な推論に基づき、考えられる解の探索空間に特定の数学的な制限をかけます。これにより、限られた観測からでも意味のある外挿が可能になります。

多層パーセプトロン（MLP）のような基本的なニューラルネットワークは、この誘導バイアスが最小限であるため、その強力な表現力を発揮するためには膨大なデータが必要になります。これに対し、現代の専門的な深層学習アーキテクチャは、データの構造（例えば、画像における並進不変性や、銀河カタログにおける点の順序の不変性）に関する物理的な仮定をアーキテクチャ設計に直接組み込むことで、探索空間を効果的に制約し、データ効率性を高めています。

物理的構造を符号化するアーキテクチャ

深層学習が限られたデータから効率的に学習し、一般化を可能にする鍵は、学習アルゴリズムを特定の解に導く誘導バイアス（Inductive Bias）をモデル構造に組み込むことです。このバイアスは、特定のデータタイプに内在する物理的な対称性や構造を反映した、アーキテクチャの特徴によって具現化されています。特定のデータ構造に合わせて設計されたアーキテクチャを採用することで、ネットワークは巨大な仮説空間（探索空間）を効果的に制約し、データ効率性を高めることができます。

畳み込みニューラルネットワーク (CNN)

畳み込みニューラルネットワーク（CNN：Convolutional Neural Networks）は、画像データ解析の標準的な手法です。CNNが持つ主要な誘導バイアスは並進不変性 (Translation Invariance)です。これは、画像内のどの位置に天体があっても、その特徴は同じフィルターで検出されるべきであるという物理的な仮定に基づいています。

CNNは、学習可能なフィルター（カーネル）を空間全体で共有する重み共有（Weight Sharing）によって、この不変性を実現します。この階層的な特徴学習プロセスを通じて、ネットワークは初期層でエッジやテクスチャといった局所的な特徴を捉え、より深い層に進むにつれて、より複雑な銀河の形態などの大域的な特徴を効率的に符号化していきます。

Transformerアーキテクチャ

スペクトルデータのように、データ内の要素間で長距離の依存性が重要な役割を果たす場合、Transformerアーキテクチャは非常に強力な解決策となります。スペクトル解析においては、離れた波長に現れる吸収線や輝線が、しばしば同じ原子物理学的な現象によって結びついており、これらのグローバルな関係性を捉えることが不可欠です。

Transformerの持つ誘導バイアス（設計思想）は、データ全体におけるグローバルな接続性と、「どの入力に注目すべきか」を学習するアテンション（注意）機構です。

Transformerは、このアテンションメカニズムを通じて、系列内のすべての入力間の関係を同時に計算します。これにより、従来のRNN（リカレントニューラルネットワーク）が情報を順番に処理・圧縮する過程で失いがちだった長距離の依存関係を効果的に捉え、高い診断能力を持つ特定の波長に「注意を払う」ことが可能になります。

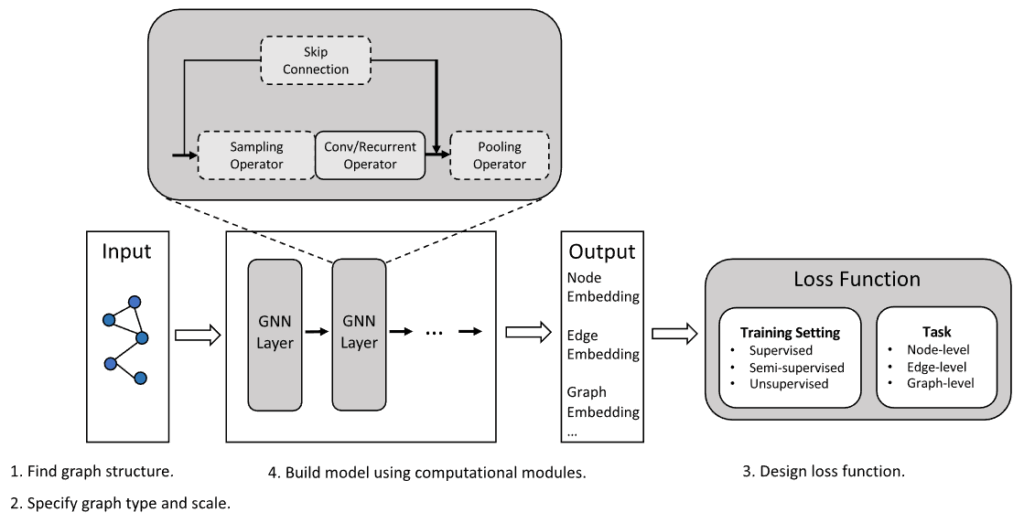
グラフニューラルネットワーク (GNN)

グラフニューラルネットワーク（GNN：Graph Neural Networks）は、銀河カタログやダークマターハローのように、順序が任意で不規則に分布する離散的なオブジェクト間の関係性をモデル化するのに適しています。

GNNの重要な誘導バイアス（設計原則）は、順列不変性 (Permutation Invariance)と局所的な集約（Local Aggregation）です。この順列不変性により、カタログ内の天体の順序がどのように変わっても、モデルの出力結果が変わらないことが保証されます。

GNNは、ノード（天体）とエッジ（関係性）を持つグラフ上で、「メッセージパッシング（Message Passing）」と呼ばれるメカニズムを通じて機能します。具体的には、各ノードは隣接するオブジェクトから情報を受け取り（集約）、自身の表現（特徴量）を更新します。

このプロセスを通じて、銀河の特性が単純な空間距離だけでなく、周囲のダークマター環境のような複雑な関係性に依存するかどうかを学習することが可能になります。

物理的な制約と方程式の組み込み

深層学習を、単にデータからパターンを抽出するだけでなく、より確実に科学的知識を生成するツールにするためには、アーキテクチャによる誘導バイアスの導入を超えて、物理法則を明示的にモデルに組み込むことが重要です。これにより、モデルは訓練データがカバーしていない領域（例えば、時間外や未観測の物理条件）へ一般化する能力が向上します。

物理的対称性の符号化 (Equivariance/Invariance)

物理学において、対称性とは、ある変換（例えば、回転や並進）を行ってもシステムの性質が不変に保たれることを意味します。ニューラルネットワークは、この対称性を2つの主要な概念で符号化できます。

1つは不変性 (Invariant) です。これは、入力が変換されても出力が変わらないことを指します。例えば、銀河の形態分類の結果（渦巻き銀河であること）は、画像を回転しても同じであるべきです。

もう1つは同変性 (Equivariant) です。これは、出力が入力と同じように変換されることを指します。例えば、銀河の渦状腕を検出する特徴マップは、入力画像が90度回転したら、対応して90度回転する必要があります。

この同変性をモデルに組み込むことで、ネットワークは、同じフィルターセットをすべての向きで共有して利用できるため、学習に必要なパラメーターの数やトレーニングデータを大幅に少なくできます。また、乱流や大規模構造のべき乗則が示すスケール不変性を符号化することでも、サンプル効率の向上が示されています。

物理情報付きニューラルネットワーク（PINN）

物理法則を組み込むより直接的なアプローチとして、物理情報付きニューラルネットワーク（PINN：Physics-Informed Neural Networks）があります。深層学習は勾配降下法で訓練されるため、ネットワーク全体が微分可能であるという特性を利用し、微分方程式や保存則を制約として組み込みます。

具体的には、ネットワークの学習目標である損失関数 $L$を拡張します。

$$L = L_{data} + \lambda_{physics}L_{physics}$$

ここで、\(L_{data}\) は観測データとの誤差を測る項、\(L_{physics}\) はモデルが物理方程式をどの程度破っているかを測るペナルティ項です。\(\lambda_{physics}\)という重み付け係数によって、データ適合性と物理法則の遵守をバランスさせながら学習を進めます。

これにより、ネットワークは観測データに適合するだけでなく、同時に物理法則を尊重する解を見つけ出します。従来の解析手法が特定の関数形式（例：銀河のポテンシャルを推論する際の等温球モデル）を仮定せざるを得なかったのに対し、PINNは銀河の運動学から重力ポテンシャルを非パラメトリックに推論できます。これは、恒星大気の静水圧平衡や銀河風のダイナミクスなど、複雑な物理システムを制限的な仮定なしにモデル化するための強力な手段となります。

SBIとマルチスケールモデリング

深層学習を宇宙物理学における最も困難な課題、特にシミュレーションと観測の間のギャップを埋めるために活用する場合、これまでに議論したアーキテクチャや制約といった構成要素が組み合わされ使用されます。

マルチスケール・モデリングとサロゲート・シミュレーション

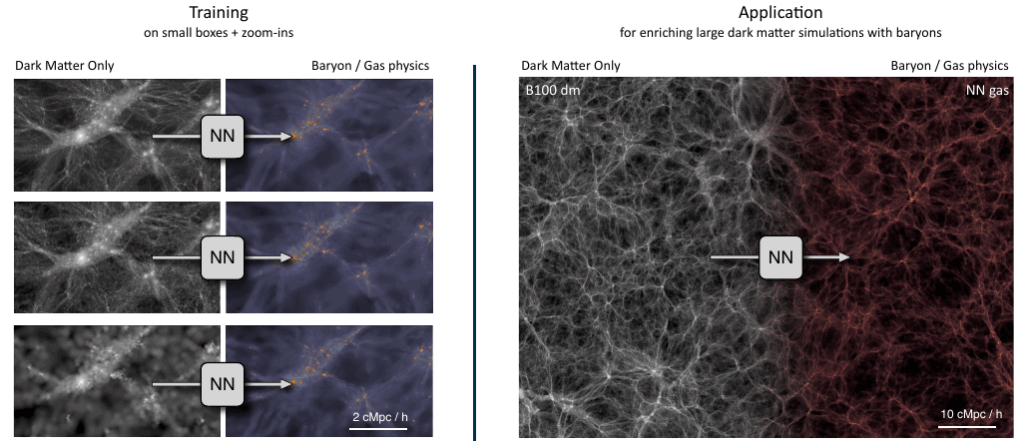
銀河形成のようなシステムは、10桁以上のスケールにまたがっているため、単一のシミュレーションで全スケールを解像することは計算上不可能です（これは解像度とボリュームのトレードオフとして知られています）。このため、シミュレーションの解像度よりも細かいスケールで起こる物理現象（サブグリッド物理：Subgrid Physics）は、通常、パラメトリックな近似に頼らざるを得ませんでした。

深層学習は、このサブグリッド物理をデータ駆動型で学習するための代替モデルとして機能します。計算コストの高い高解像度シミュレーションから効果的な理論（モデル）を学習し、それを計算コストの低い大規模シミュレーションへと適用（ペイント）します。

この目的に適したアーキテクチャの一つがU-Netです。U-Netは、エンコーダー・デコーダー型のネットワークにスキップ接続（Skip Connections）を追加した構造をしています。

• エンコーダーは、大規模環境のような大局的なコンテキストを捉えます。
• スキップ接続により、個々の銀河の位置といった微細な空間情報を保持することが可能です。

U-Netは、バリオン化の問題において特に優れた性能を発揮します。これは、ダークマター密度のフィールドを入力として、対応するガス密度や中性水素密度を予測するように訓練されます。この学習済みモデルを利用することで、流体力学の実行が計算上困難な大規模なダークマターシミュレーションに対しても、現実的なバリオン物理を組み込むことが可能になります。

シミュレーションに基づく推論（SBI）

マルチスケール・モデリングによって得られる複雑なシミュレーションモデルは、新たな課題を提起します。それは、観測データ \(d\) が与えられたとき、その尤度（Likelihood） \(p(d|\theta)\) を解析的に計算することが不可能であるという問題です。

非線形な宇宙論的構造形成や複雑な系外惑星大気モデルなど、現代の複雑なシステムにおいては、ベイズ推論に不可欠な尤度を扱うことができません。

シミュレーションに基づく推論（SBI：Simulation-Based Inference）は、この課題を克服するために開発されました。

SBIは、大量のシミュレーション（パラメーター \(\theta\) とシミュレーションデータ \(d_{sim}\) のペア）を実行し、ニューラルネットワークを用いて事後分布 \(p(\theta|d)\) や尤度 \(p(d|\theta)\) を直接近似学習します。

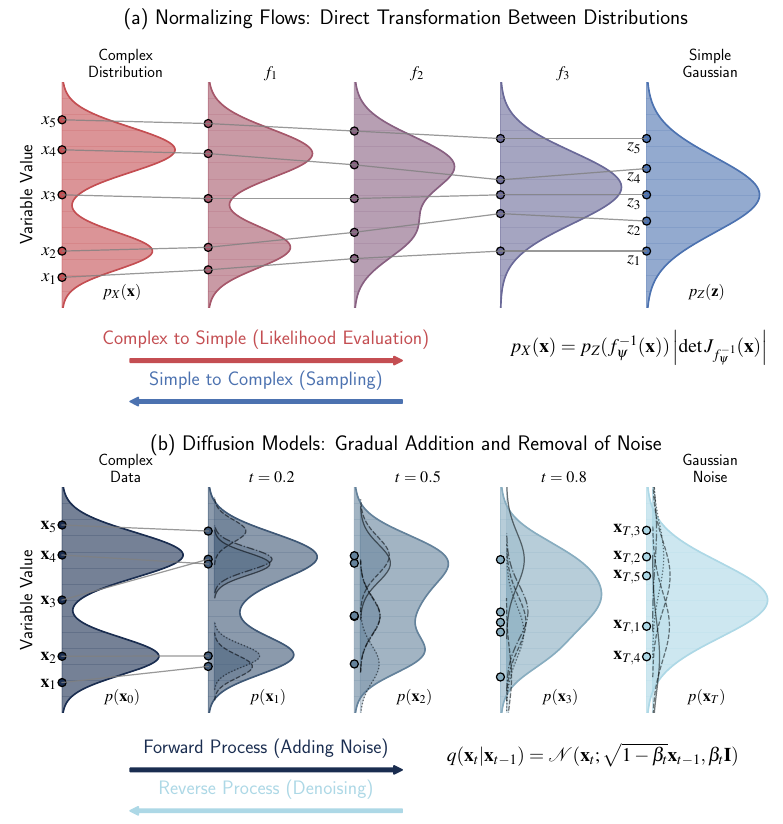
この実装技術の核となるのが、正規化フロー（Normalizing Flows: NF）です。

• 正規化フローは、複雑な確率分布を単純なガウス分布に変換する可逆なニューラルネットワークです。
• これにより、安定した密度推定と厳密な尤度計算が可能になります。

SBIの導入による研究への利点は多大です。

1. 計算コストの償却（Amortization）: 従来のマルコフ連鎖モンテカルロ法（MCMC）が数日を要した系外惑星の大気推論を、学習済みの正規化フローは数秒で実行できます。これにより、推論の計算コストを償却できます。
2. 情報圧縮の回避: 要約統計量に情報を圧縮することなく、フィールドレベルの宇宙論的推論を可能にします。これにより、非ガウス的な複雑な情報も最大限に活用できるようになります。

おわりに

深層学習は、現代の宇宙物理学におけるデータ解析のツールキットを強力に拡張するものです。古典的な統計的手法がスケーラビリティ、表現力、データ効率の間のトレードオフに直面するのに対し、深層学習は、物理的な知識をモデル構造（アーキテクチャ）や制約として組み込むことで、これらの特性を同時に達成することを目指しています。

研究では、アーキテクチャの選択（例：CNN 対 Transformer）を通じて、どの物理原理を厳密な制約として組み込むか、そしてどれをデータ駆動的な柔軟性のために残すかというバランスにかかっています。

物理情報付きニューラルネットワーク（PINN）の損失関数に含まれるハイパーパラメーター \(\lambda_{\text{physics}}\) は、理論的な事前知識をどの程度強く強制するかを制御する役割を果たします。最も成功しているアプローチは、この物理的知識とデータ駆動型の柔軟性を統合しています。 実用的な課題の一つは、天文学において結果の信頼性を確保するために不可欠な不確実性の定量化の難しさですが、深層学習は、アノマリー検出やオペレーションの最適化といった新たなフロンティアを開いています。

例えば、VAEや正規化フローなどのニューラル密度推定器を用いて、高速電波バーストのような未知の現象（アノマリー）を系統的に特定できます。また、強化学習（RL）は、ヒューリスティックなルールを上回る、複雑な望遠鏡のスケジューリングや補償光学制御のための最適戦略を学習できます。 深層学習は統計的手法を置き換えるものではなく、その上に構築される強力な追加ツールです。

More Information

• arXiv:2510.10713, Yuan-Sen Ting, 「Deep Learning in Astrophysics」, https://arxiv.org/abs/2510.10713