Home > Blog > データサイエンス > 次元削減の罠: なぜt-SNEやUMAPを誤用するのか？

次元削減の罠: なぜt-SNEやUMAPを誤用するのか？

データ探索や可視化の現場において、t-SNEとUMAPはデファクトスタンダードとしての地位を確立しています。多くの実務者が、高次元データの構造を理解するためにこれらのアルゴリズムを信頼し、クラスター分析や異常検知といった重要なタスクに活用しています。ですが、その信頼は本当に正当なものでしょうか？

近年の研究は、これらの手法が私たちの直感に反する挙動を示し、データサイエンティストを誤った解釈へと導くリスクがあることを指摘しています。例えば、ランダムなノイズから意味ありげなクラスターを作り出したり、逆に重要な外れ値を集団の中に隠蔽してしまったりすることが数学的にも示されています。

本記事では、t-SNEとUMAPが抱える「クラスターの捏造と消失」、「外れ値の隠蔽」、そしてなぜこれほどまでに「誤用」が広がってしまったのかというメカニズムについて、最新の研究成果をもとに解説します。

1. クラスターは「捏造」され、そして「消失」する

可視化結果に現れる鮮やかなクラスター構造が、必ずしも元のデータの構造を正しく反映しているとは限りません。t-SNEやUMAPが生成するプロットは、時に私たちを欺き、存在しないパターンを見せたり、逆にあるはずのパターンを隠してしまったりすることが、最新の研究で明らかになっています。

存在しないクラスターの捏造 (False Positives)

「ランダムなノイズデータから、意味ありげなクラスターが現れる」。これは単なる目の錯覚ではなく、数学的に証明されたt-SNEの性質です。

Bergamらの研究（2025）によると、高度にクラスター化されたデータが生み出す可視化結果と、全くクラスター構造を持たない「偽のデータセット（impostor dataset）」が生み出す可視化結果が、完全に一致するケースが存在します。つまり、t-SNEの出力結果（目的関数の停留点）だけを見ても、元のデータが本当にクラスター構造を持っていたのか、それとも単なるランダムな点群だったのかを判別することは理論的に不可能なのです。 したがって、可視化されたマップ上でクラスターが分かれているからといって、「データには明確なグループ分けが存在する」と早合点するのは非常に危険です。それはアルゴリズムが作り出した「幻影」かもしれません。

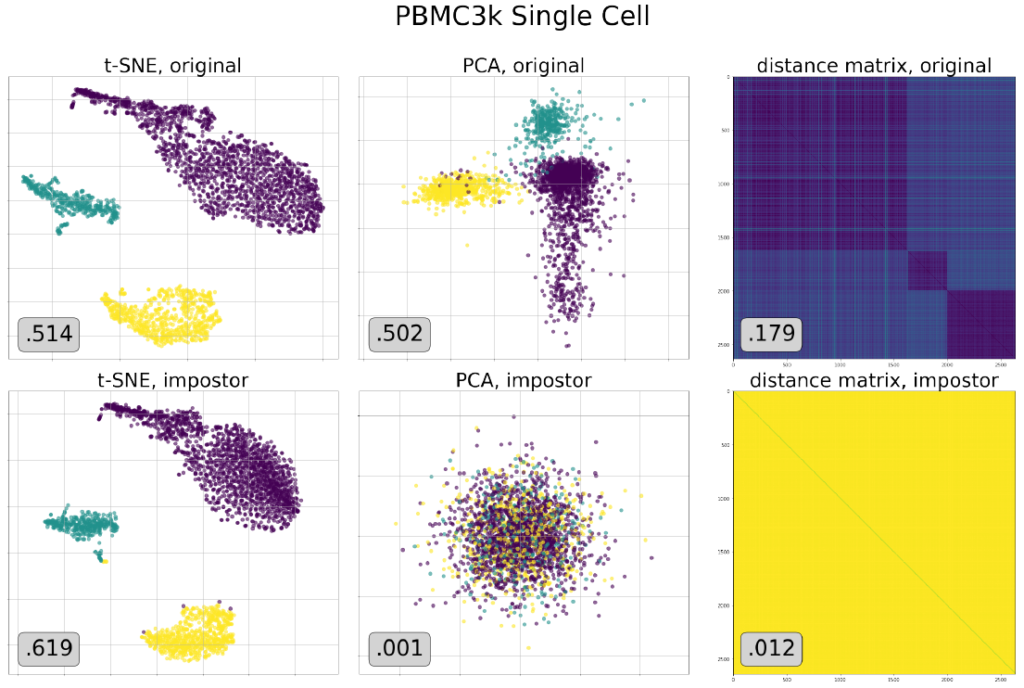
図1. 単一細胞データ（上段）と任意にクラスター化された偽造データセット（下段）の可視化。2D t-SNE可視化（左列）では、どのデータセット（実データまたは偽造データ）からプロットが生成されたかを区別することは困難である。高次元点間距離（右列）をプロットすると、偽造データセットが実際にはクラスター化されていないことが確認できる。参考として、他の手法ではこの問題が発生しないことを示すため、2D PCA可視化（中央列）も示している。各図の左下の数字は、実データ（上段）と偽造データ（下段）における2D t-SNEプロット（左列）、2D PCAプロット（中央列）、および高次元入力（右列）の平均シルエットスコアによるクラスターの顕著性を示す。すべての散布図の色分けは、左上のt-SNEプロットに対するDBSCANクラスタリング（Ester et al., 1996）に対応している。

存在するクラスターの消失 (False Negatives)

「捏造」とは対照的に、明確なクラスター構造を持つデータであるにもかかわらず、t-SNEがそれを表現できずに単一の塊（blob）として描画してしまう「消失」の問題も深刻です。

Yangらの研究（2021）では、SHUTTLEやIJCNNといった明確なクラスター構造を持つ実データセットに対し、t-SNEがクラスターを分離できず、ただの球状や毛玉のような塊として表示してしまう事例が報告されています。 さらに驚くべきことに、この問題は「使い方が悪い」せいではありません。パープレキシティ（perplexity）などのハイパーパラメータを広範囲に調整しても、あるいは最適化アルゴリズムを改良してより良い局所解を見つけたとしても、クラスター構造は現れないことが示されています。これは、t-SNEの目的関数自体が、特定のデータ分布においてはクラスターを保持するように設計されていない可能性を示唆しています。

ポイズニングへの脆弱性

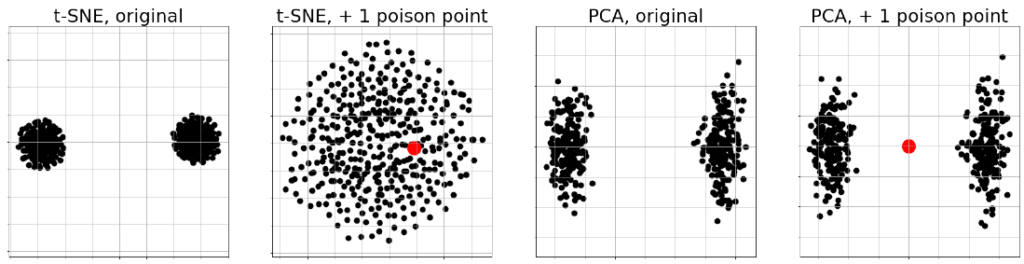
さらに、t-SNEはデータの局所的な変化に対して極めて敏感であることも分かっています。Bergamらは、明確に分離された2つのクラスターを持つデータセットに対し、たった1点の「ポイズニング（毒）」となる点を追加するだけで、可視化結果のクラスター構造が劇的に破壊されることを示しました。 本来であれば、数千件のデータの中に1件の異常値が混ざったとしても、全体の大域的な構造は保たれるべきです。しかしt-SNEにおいては、そのわずかな変化が全体の配置に波及し、本来見えるはずだった構造をかき消してしまうリスクがあるのです。

2. 外れ値はどこへ消えたのか？

「データの分布を確認するために、とりあえずt-SNEで可視化してみよう」。そう考えて異常検知や外れ値分析に取り組んでいるのであれば、今すぐ立ち止まる必要があります。t-SNEは、そのアルゴリズムの特性上、重要な外れ値を「なかったこと」にしてしまう危険性を孕んでいるからです。

外れ値の過小評価：バルクへの埋没

t-SNEが生成する美しいクラスター構造の裏で、極端な外れ値（Outliers）がどのような扱いを受けているかご存知でしょうか。最新の理論研究（Bergam et al., 2025）は、t-SNEが入力データの外れ値を適切に表現できず、主要なデータ群（バルク）の中に埋没させてしまう傾向があることを証明しました。

PCA（主成分分析）と比較すると、その違いは歴然です。PCAはデータの大域的な分散を最大化するように射影するため、平均から極端に離れたデータ点は、可視化結果においても「遠く離れた点」として描画されます。一方、t-SNEは「近傍」の関係性を維持することに注力します。高次元空間で孤独な外れ値であっても、低次元空間（出力）では確率分布の整合性を取るために、無理やり誰か（他のデータ点）の近くに配置されようとする力が働きます。その結果、本来は遥か彼方にあるはずの異常値が、あたかも正常なクラスターの一部であるかのように取り込まれてしまうのです。

図2. 入力データセットに単一の「ポイズン」ポイントを挿入した場合のt-SNEおよびPCAプロット。

不正検出などへの不適合

この性質は、実務において致命的なミスリードを引き起こす可能性があります。例えば、クレジットカードの不正利用検出のようなタスクを想像してください。不正な取引は、数百万件の正常な取引の中にわずかに紛れ込む「極端な外れ値」です。

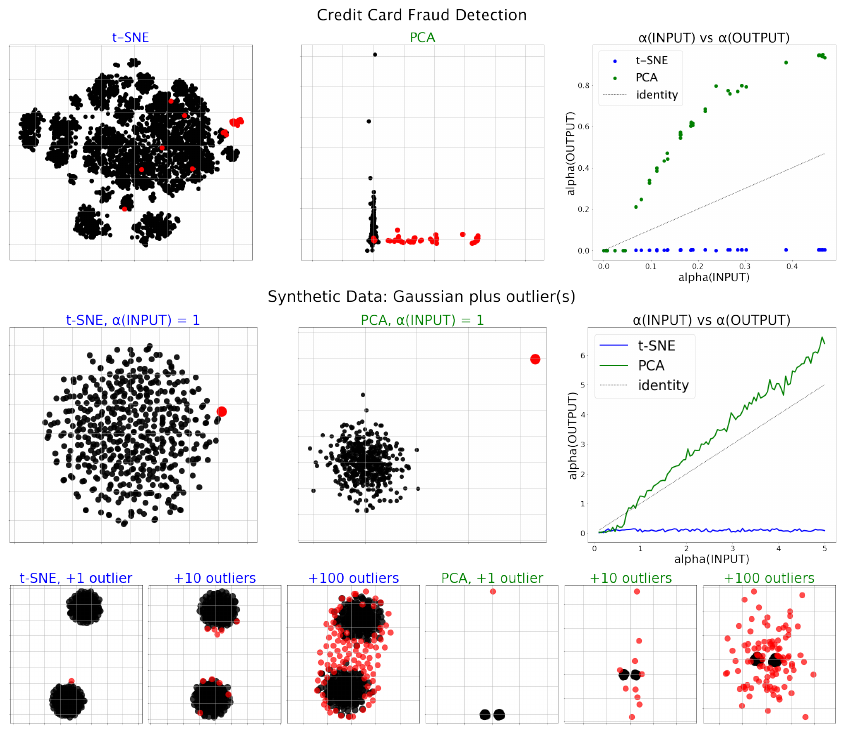
ある金融取引データを用いた実験では、PCAが不正取引（外れ値）を正常な取引から明確に分離できたのに対し、t-SNEはそれらを正常なデータの塊の中に混在させてしまいました。もし、この可視化結果だけを信じて「不正なパターンは見当たらない」と判断してしまったらどうなるでしょうか？

理論的には、入力データにおいてどれほど極端な外れ値であったとしても、t-SNEの出力においては、その「外れ度合い（α-outlier number）」が一定の範囲内（約3倍程度）に収まってしまうことが示されています。つまり、t-SNEの出力から「これは異常なデータだ」と視覚的に判断することは、数学的に困難なのです。

外れ値を見つけたいのであれば、t-SNEではなく、PCAのような大域的な構造を保持する手法を選択する、あるいは専用の異常検知アルゴリズムを併用することが賢明です。きれいなクラスター図に惑わされて、真に見るべき脅威を見落とさないように注意が必要です。

図3. t-SNEおよびPCAのα-Outlierに対する応答。上段：金融活動を追跡するデータセット（約1%が不正）において、t-SNEは不正（赤）ポイントと非不正（黒）ポイントをほぼ分離できていないが、PCAはほぼ完全に分離できている。不正データポイントは、非不正グループに対してα > 0の外れ値である。右上の図は、t-SNEおよびPCAがこれらのα値を出力にどのように反映しているかを示す。中段：ガウス分布からのサンプルと1個のα-Outlier（αの値は様々）からなる合成データセットでの同様の分析。下段：2つのガウス分布と1個、10個、100個のα-Outlierを混合したもの。外れ値と2つのクラスター間には大きなギャップ（α > 1）が存在するにもかかわらず、t-SNEはそれらを分離できない。

3. t-SNEとUMAPの数理的なつながりと違い

「t-SNEは可視化に特化しており、UMAPは多様体学習に基づいているため大域的な構造を保持する」。このような説明をよく耳にしますが、最新の研究はよりシンプルで衝撃的な事実を明らかにしています。実は、この2つのアルゴリズムは対照学習（Contrastive Learning）の観点から見ると、兄弟のような密接な関係にあるのです。

対照学習による統一的解釈

一見異なる挙動を示す両者ですが、数理的には以下のように整理できます。

  • t-SNE: 「ノイズ対照推定（Noise-Contrastive Estimation: NCE）」を用いた手法。
  • UMAP: 「負例サンプリング（Negative Sampling: NEG）」を用いた手法。

Damrichらの研究（2022）によると、UMAPの実装は、本質的に「t-SNEのフレームワークに負例サンプリング（NEG）を適用したもの」と解釈可能です。つまり、両者の違いは「次元削減の哲学」の違いというよりは、最適化における「損失関数の形式」の違いに大きく依存しています。

図4. MNIST データセットに対する Neg-t-SNE の埋め込みスペクトル（a–e）。固定正規化定数 (\(\bar{Z}\)) を変化させると、(\(\bar{Z}\)) の増加に伴い埋め込みのスケールは縮小し、クラスタはよりコンパクトかつ分離するが、さらに大きくなると再び融合し始める。得られる構造は (f) t-SNE、(g) NCVis、(h) UMAP の結果と対応し、(\(\bar{Z}\)) がそれぞれの手法における分配関数や正規化パラメータ、(\(|X|/m\)) に一致すると同等の埋め込みになる。(i) は分配関数 (\(\sum_{i,j}(1+d_{ij}^2)^{-1}\)) が (\(\bar{Z}\)) に合わせて増加する様子を示す。実験では全て (\(\bar{Z}=|X|/m\)) で初期化しており、early exaggeration を用いない場合、小さな (\(\bar{Z}\)) ではクラスタが分断されやすい。

なぜUMAPのクラスターは「密」に見えるのか？

UMAPの出力結果は、t-SNEに比べてクラスターがコンパクトに凝縮され、クラスター間の空白が広く見える傾向があります。これはUMAPが優れているからというよりは、目的関数における正規化定数の扱いの違いに起因します。

  • t-SNE (NCE): 正規化定数を学習可能なパラメータとして扱い、データ分布に合わせて調整します。
  • UMAP (NEG): 正規化定数を固定された非常に大きな値として扱います。

UMAPでは、この大きな固定定数とバランスを取るために、データポイント同士の類似度（確率）を無理やり高くする必要があります。その結果、ポイント同士を引き寄せる引力が強く働き、非常に凝集度の高い「密」なクラスターが形成されるのです。

数値的な不安定性と「焼きなまし」

さらに、UMAPの損失関数を解析すると、類似度の計算において暗黙的に \(1/d^2\)（逆二乗） というカーネルを使用していることが分かります。 t-SNEが使用するコーシー分布（\(1/(1+d^2)\)）は距離が0になっても値が1に収まるのに対し、UMAPの \(1/d^2\) は距離が0に近づくと無限大に発散してしまいます。このため、UMAPは数値的に不安定になりやすく、最適化の過程で学習率を徐々に下げる「アニーリング（焼きなまし）」などの工夫が実装上不可欠です。

つまり、UMAPの「速くてきれい」な結果は、アルゴリズムの安定性を犠牲にした絶妙なチューニングの上に成り立っているとも言えるのです。

4. どのように誤用されているのか？

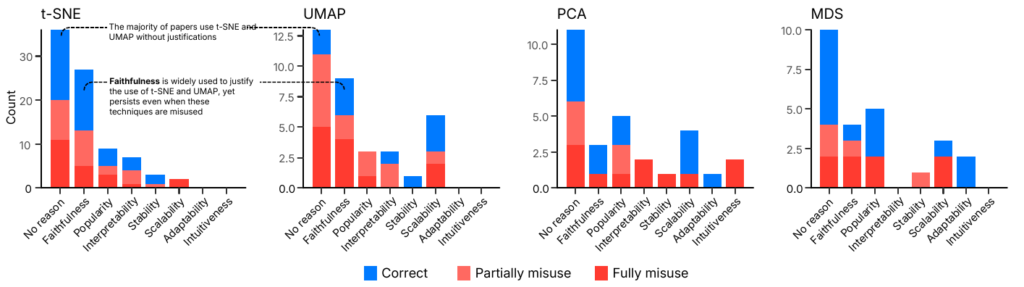
t-SNEやUMAPは強力なツールですが、それゆえに「万能なハンマー」として扱われ、釘ではないものまで打とうとしてしまうケースが後を絶ちません。最新の調査（Jeon et al., 2025）によると、視覚的分析に関する136本の論文をレビューした結果、t-SNEとUMAPが最も頻繁に「誤用」されている次元削減手法であることが判明しました。

不適切なタスクへの適用：ローカル vs グローバル

最大の問題は、これらの手法が「局所的な構造（Local Structure）」の保存に特化しているにもかかわらず、「大局的な構造（Global Structure）」の分析に使用されてしまう点にあります。

  • 得意なこと: 「ある点の近傍にどの点があるか（Neighborhood Identification）」や「クラスターがいくつあるか（Cluster Identification）」を見つけることには適しています。
  • 苦手なこと: 「クラスターAとクラスターBの距離」や「クラスターの密度」を正確に表現することは苦手です。

例えば、可視化されたプロットを見て「クラスターAとBは距離が近いから、性質も似ているはずだ」と推論したり、「このクラスターはギュッと詰まっているから密度が高い」と判断したりするのは、t-SNEやUMAPのアルゴリズム的特性上、誤った解釈を招く可能性が高いです。それにもかかわらず、多くの研究や実務で、こうしたグローバルな比較に誤って使用されているのが現状です。

図5. 次元削減を用いた分析タスクと、ローカルおよびグローバルな次元削減手法の関連性を示す図解です。文献レビューに基づき、次元削減を活用した7種類の分析タスクを特定。t-SNEやUMAPは、近傍探索、およびクラスター識別といったタスクには適していますが、それ以外のタスクには必ずしも最適ではありません。

なぜ誤用は止まらないのか？

なぜ専門家でさえもこのような誤用をしてしまうのでしょうか？ インタビュー調査からは、実務者が抱える心理的・環境的な要因が浮き彫りになりました。

  • 「査読への免疫（Immunity）」: 「t-SNEやUMAPを使っておけば、レビュワーから文句を言われない」という認識が広がっています。「皆が使っているから」「SOTA（State-of-the-art）だから」という理由で、思考停止的に選択される傾向があります。
  • 誤った推奨の連鎖: 同僚や指導教員からの勧め、あるいは先行研究の踏襲によって誤用が再生産されています。さらに近年では、ChatGPTのようなLLM（大規模言語モデル）が、文脈を考慮せずにこれらの手法を推奨することも、バイアスを強化する一因となっています。
  • ライブラリの利便性: scikit-learnなどのライブラリで極めて手軽に実装できることも、深い理解なしでの利用を助長しています。他のより適切な手法（PCAやMDSなど）よりも、t-SNEやUMAPの実装の方が「手っ取り早い」環境が、誤用を招いている側面があります。

多くの論文では、これらの手法を選択した理由として「Faithfulness（忠実性）」を挙げていますが、実際にはグローバルな構造に対して忠実ではないため、矛盾した正当化が行われていることになります。

図6. 次元削減技術の適切または不適切な使用に関する推論別の件数。 各推論（x軸）は、t-SNE（左端のグラフ）の使用根拠として引用された頻度に基づき、降順で配置されています。

おわりに

t-SNEとUMAPは、高次元データの探索において極めて強力な武器となりますが、決して万能な「魔法の杖」ではありません。これらのアルゴリズムは、局所的な近傍関係を強調して可視化するあまり、大域的な位置関係を歪めたり、重要な外れ値を隠蔽したりするリスクを常に孕んでいます。

データサイエンティストとして、我々は以下の点に留意する必要があります。

  1. 盲信しない: 画面上の美しいクラスターはアルゴリズムが生み出した「幻影」かもしれませんし、重要な異常値が通常のデータの中に埋没している可能性もあります。結果を批判的に見る姿勢が不可欠です。
  2. 大域的な評価には別の手法を: クラスター間の距離やデータの密度を議論したい場合は、PCAやMDSといった大域的な構造を保持する手法、あるいはdensMAPのような特化したツールを併用してクロスチェックを行うべきです。
  3. ツールの特性理解: UMAPがt-SNEよりも「密」なクラスターを作るのは魔法ではなく、数理的な最適化手法（NEG vs NCE）と正規化定数の扱いの違いによる必然的な結果であることを理解しましょう。

将来的には、タスクに応じて最適な次元削減手法を自動で提案してくれるシステムの登場も期待されています。しかし、そのような未来が到来するまでは、私たち自身がツールの限界を正しく理解し、出力された結果を読み解くリテラシーを持つことが、信頼できる分析への唯一の道なのです。

More Information

関連記事

機械学習モデルにおける不確実性

今日、機械学習モデルは、私たちの生活やビジネスのあらゆる側面に浸透しています。しかしながら、その高い予測精度とは裏腹に、モデルの信頼性や頑健性には依然として重大な課題が残されています。 実際、レベル5の自動運転車がカメラ […]

iLTM: 表形式データ向けの大規模基盤モデル

表形式データのモデリングにおいて、長らく実務のデファクトスタンダードとして君臨してきたのは勾配ブースティング決定木（GBDT）でした。画像や自然言語の分野で深層学習が席巻する中、表形式データだけは「GBDTが最適解」とい […]