長年にわたり、多層パーセプトロン（Multi-Layer Perceptron, MLP）は、回帰分析、関数近似、パターン認識といった様々なタスクで中心的な役割を果たしてきました。しかし、その一方で、MLPにはいくつかの課題も指摘されています。例えば、活性化関数が固定されているために関数の表現力に限界があること、ネットワークの内部構造が複雑で解釈が難しいこと、そして高い精度を達成するためには膨大な数のパラメーターが必要になることなどです。

こうした課題への新しいアプローチとして、近年、コルモゴロフ・アーノルド・ネットワーク（Kolmogorov-Arnold Networks, KANs） が有望な代替技術として注目を集めています。このネットワークは、20世紀の著名な数学者アンドレイ・コルモゴロフとウラジーミル・アーノルドによる「コルモゴロフ・アーノルド表現定理」に着想を得ています。

MLPがニューロン（ノード）上で固定された活性化関数を用いるのに対し、KANはネットワークのエッジ（接続）上に学習可能な単変量関数（univariate basis functions） を配置するという、全く異なるアプローチを採用しています。この構造的な違いが、KANに高い表現力と解釈性をもたらします。

この記事では、KANの基本的な構造からMLPとの違い、そして実際の応用で役立つ設計戦略までを、分かりやすく解説していきます。

1. KANの基礎: MLPとの構造的な違い

KANとMLPは、どちらも入力から出力を計算するための階層的な関数近似器ですが、その計算プロセス、特に非線形性をどのように扱うかという点で根本的に異なります。

• MLPの仕組み: MLPでは、まず入力信号が重み付けされて足し合わされ（線形結合）、その結果が固定の非線形活性化関数（ReLUやtanhなど）に通されます。このプロセスは「mix → activate」と表現でき、数式では以下のように表されます。
  $$
  \mathbf{z}^{(l+1)} = \sigma(\mathbf{W}^{(l)}\mathbf{z}^{(l)} + \mathbf{b}^{(l)})
  $$
  ここで、\(\mathbf{z}^{(l)}\) は第 \(l\) 層からの出力、\(\mathbf{W}^{(l)}\) と \(\mathbf{b}^{(l)}\) はそれぞれ重み行列とバイアス、\(\sigma\) はReLUのような固定の活性化関数です。入力がまず線形変換（mix）され、その後まとめて非線形活性化（activate）されていることがわかります。
• KANの仕組み: 一方、KANでは、まず各入力信号が個別に（学習可能な）1次元の関数によって変換され、その変換後の信号が単純に足し合わされます。これは「activate → mix」という逆のプロセスです。KANの1層の処理は、以下の数式で表現されます。
  $$
  x_q^{(l+1)} = \sum_{p=1}^{N_l} \phi_{q,p}^{(l)}(x_p^{(l)})
  $$
  ここで、\(x_p^{(l)}\) は第 \(l\) 層の \(p\) 番目のニューロンからの出力です。重要なのは \(\phi_{q,p}^{(l)}\) の部分で、これは第 \(l\) 層の \(p\) 番目のニューロンと第 \(l+1\) 層の \(q\) 番目のニューロンを繋ぐエッジ上に定義された、学習可能な関数です。入力 \(x_p^{(l)}\) はまず個別に非線形変換（activate）され、その結果が単純に合計（mix）されています。この \(\phi\) をB-スプラインやチェビシェフ多項式といった基底関数で表現することで、KANは非常に高い表現力を獲得します。

この計算順序の転換により、KANはMLPよりも局所的な特徴を捉えやすく、解釈性の高いマッピングを学習することが可能になります。

パラメーター効率の優位性

理論的な研究では、KANは同等の表現力を持つMLPと比較して、より少ないパラメーターで済む、優れたパラメーター効率を持つことが示されています。特に、B-スプラインのような基底関数を細かいグリッドで用いる場合、その効率はさらに向上します。これは、固定された単純な非線形関数（点）で複雑な関数を近似するMLPよりも、学習可能な曲線（線）で近似するKANの方が、より効率的にターゲット関数を表現できるためと考えることができます。

2. KANの心臓部：多様な基底関数

KANの性能を決定づける最も重要な要素は、エッジ上で学習される単変量関数 \(\phi\) をどのように表現するか、すなわち基底関数（basis function） の選択です。この選択肢の多様性こそが、KANを単なるMLPの代替ではなく、柔軟な問題解決ツールたらしめている理由です。

2.1 主要なKANバリアントとリソース

研究の進展に伴い、様々な特性を持つ基底関数を用いたKANのバリアントが提案されています。以下に代表的なものをまとめます。

種類 (KAN Variant)	基底関数 (Basis Function)	特徴・主な用途	主要な論文/リポジトリ
Official KAN	B-スプライン (B-spline)	局所性、滑らかさ、高い解釈性。あらゆるタスクの標準的なベースライン。	Liu et al., 2024 pykan
ChebyKAN	チェビシェフ多項式	グローバル性、直交性、スペクトル近似特性。滑らか、または振動的な関数、PDEソルバーに適する。	Mahmoud et al., 2025 ChebyKAN
ReLU-KAN / HRKAN	ReLUの合成	計算効率が非常に高い（B-スプラインの5〜20倍高速）。GPUに優しい。	Qiu et al., 2024 relu_kan
FourierKAN / KAF	フーリエ級数/特徴	周期的な関数や大域的な特徴を持つデータのモデリングに強力。	Xu et al., 2024 FourierKAN / KAF
FastKAN (Gaussian RBF)	ガウスRBF	B-スplinesの高速で滑らかな代替。局所的な特徴抽出に優れる。	Li, 2024 fast-kan
SincKAN	Sinc関数	不連続性、特異点、急峻な勾配を持つ関数の近似に特化。	Yu et al., 2024 SincKAN
Wav-KAN	ウェーブレット	マルチスケール解析。局所的なバーストや不均一なデータ構造を持つ信号の解析に適する。	Bozorgasl & Chen, 2024 Wav-KAN

2.2 実務的な選択指針

どの基底関数を選ぶべきか、いくつかの指針を以下に示します。

• 安定性を重視する場合: まずは立方B-スプラインをデフォルトとして試すのが良いでしょう。振動的な関数を扱う場合は、ChebyKAN（入力にtanh正規化を適用）がより安定した学習をもたらすことがあります。
• 計算速度を優先する場合: ReLU-KANやガウスRBF (FastKAN) が適しています。これらはGPU上での並列計算と相性が良く、学習時間を大幅に削減できる可能性があります。
• 物理シミュレーションなど（PDEs）: チェビシェフ多項式やヤコビ多項式は、高次の導関数を扱う際に数値的に安定しており、従来のMLPベースの手法よりも高速な収束が期待できます。

3. KANの拡張と高度な応用戦略

KANの設計思想は非常にモジュール性が高く、MLPの代替としてだけでなく、畳み込みニューラルネットワーク（CNN）、トランスフォーマー、グラフニューラルネットワーク（GNN）といった、様々なアーキテクチャに組み込むことが可能です。

3.1 KANの適用分野

KANの構成要素は、以下のような幅広い分野で、既存のMLPブロックを置き換える「ドロップイン代替」として利用され、モデルの解釈性や効率を向上させています。

• 科学技術計算 (PIKANs): 物理法則を組み込んだニューラルネットワーク（PINNs）の活性化関数を、学習可能な基底関数（B-スプラインやチェビシェフ）に置き換えることで、解の局所的な振る舞いをより正確に捉え、解釈性を高めます。例えば、作用素学習モデルであるDeepONetのKAN版、DeepOKANなどが提案されています。
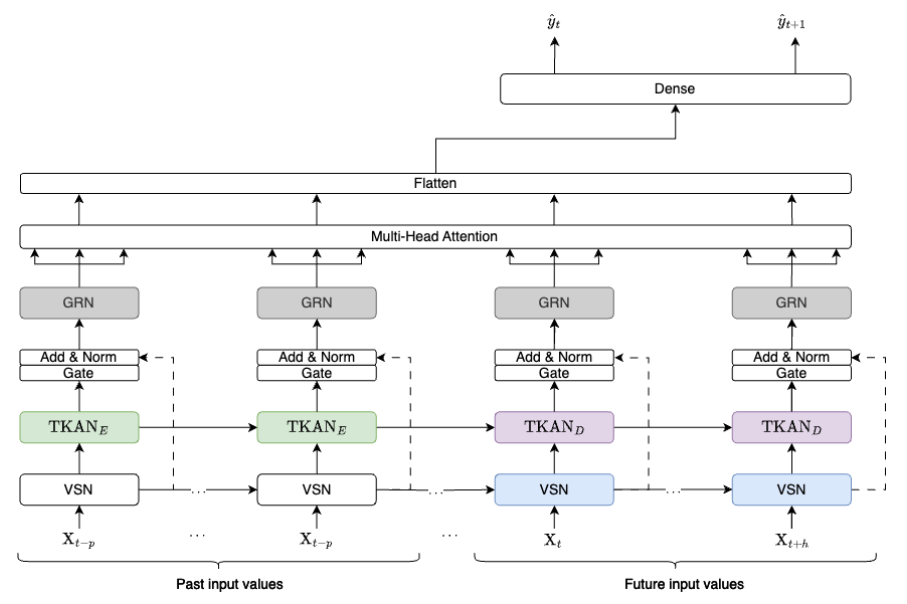
• 時系列・シーケンシャルモデリング: KANをアテンション層に統合したトランスフォーマーモデル（TKAT）や、フーリエ級数展開を利用した時系列異常検知モデル（KAN-AD）など、シーケンシャルデータの複雑なパターンを捉えるための応用が進んでいます。
• グラフ・構造化データ: GNNのメッセージパッシング処理にKAN層を導入することで、ノード特徴の変換をより柔軟にし、数値的な安定性と表現力を向上させる試み（GraphKAN）が行われています。

3.2 精度と安定性を高めるための戦略

実務でKANの性能を最大限に引き出すには、基底関数の選択だけでなく、学習プロセスそのものを工夫することも重要です。

• ハイブリッド最適化: 学習の初期段階では Adam や RAdam のような適応的勾配法を用いて大域的な解の探索を行い、その後 L-BFGS のような準ニュートン法に切り替えて解の精度を高めるというハイブリッドスケジュールが有効です。特に、物理シミュレーションのような問題を解く際に、収束速度と最終的な精度の両方を改善することが報告されています。
• アダプティブ・サンプリングとグリッド調整:
  • 自由ノット適応 (Free-knot adaptation): B-スプラインのノット（結び目）の位置を固定せず、学習データに応じて自動的に調整する手法です。これにより、関数の変化が激しい領域にノットが集中し、より効率的な近似が可能になります。
  • 残差に基づく適応的サンプリング (RAD): 物理シミュレーションにおいて、PDE（偏微分方程式）の残差が大きい、つまりモデルの予測が物理法則と大きく乖離している領域から重点的にサンプリングを行う手法です。これにより、モデルの学習リソースを最も困難な部分に集中させることができます。
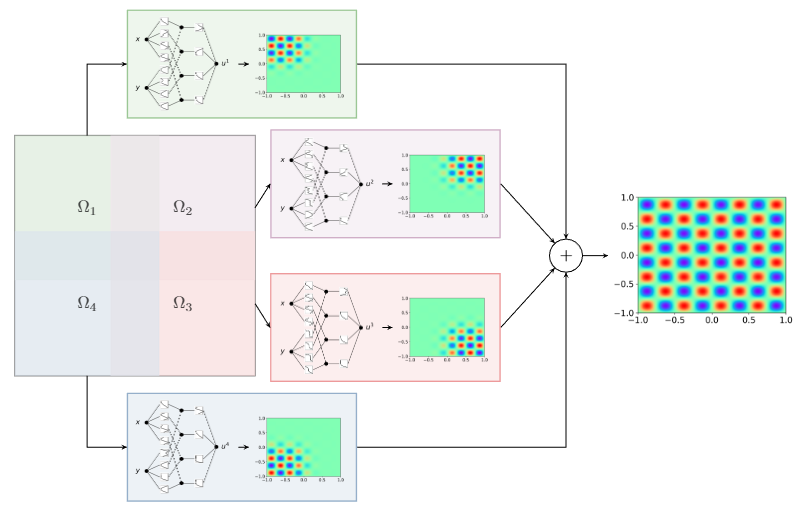
• ドメイン分割 (FBKAN): 複雑な問題領域を、重複する複数の部分領域（サブドメイン）に分割し、それぞれに軽量なローカルKANを割り当てるアプローチです。各ローカルKANの出力は、単一性の分割（Partition of Unity, PoU） と呼ばれる滑らかな関数で重み付けされて結合されます。これにより、大規模な問題の並列学習が可能になり、学習の安定性も向上します。

おわりに

コルモゴロフ・アーノルド・ネットワークは、ネットワークのエッジ上に学習可能な単変量関数を配置するという独自のアプローチにより、従来のMLPとは一線を画す、強力で柔軟な関数近似フレームワークです。この構造は、特にパラメーター効率の向上と、学習された関数の高い解釈性という点で、実用上大きな利点をもたらします。

しかし、KANの真の強みは、単一の固定されたアーキテクチャにあるのではなく、問題の性質に応じて最適な基底関数をモジュールのように選択・適応できる柔軟性にあります。例えば、滑らかな関数にはB-スプラインを、周期的な現象にはチェビシェフ多項式を、そして高速な学習が求められる場面ではReLU-KANやガウスRBFを選ぶといったように、問題の特性と利用可能な計算資源を考慮した「基底中心」の設計こそが、KANの性能を最大限に引き出す鍵となります。

この柔軟性は、ニューラルネットワークの設計思想を、まるで「汎用的な定規とコンパスのセット」（MLP）から、「問題に合わせて調整可能な様々な道具（スプライン、チェビシェフ、Sincなど）が揃った大工道具箱」 へと進化させるものと捉えることができます。最適な道具を選ぶことで、私たちは複雑な形状を持つ関数を、より正確に、かつ少ない労力で（効率的に）作り上げることが可能になるのです。

KANの研究分野は今まさに急速な発展の途上にあります。今後は、単純な「KAN 対 MLP」という性能比較を超えて、基底関数の選択理論、最適化手法、そしてネットワークの階層構造がもたらす効果など、より体系的な設計科学へと深化していくことが期待されます。

More Information

• arXiv:2510.25781, Amir Noorizadegan, Sifan Wang, Leevan Ling, 「A Practitioner’s Guide to Kolmogorov-Arnold Networks」, https://www.arxiv.org/abs/2510.25781