2009年、神経科学の世界に衝撃的な報告がなされました。MRI装置の中に入れられた「死んだ鮭」が、人間の写真に対して感情反応を示す脳活動を見せたのです。もちろん、鮭に意識があったわけではありません。これは多重比較の補正を欠いた統計処理が生み出した「幻影」であり、データ分析における重要な教訓となりました。

現在、AIの解釈性（Interpretability）手法もまた、この「死んだ鮭」の問題に直面しています。Feature AttributionやProbing、さらには最新のSparse Autoencoders（SAE）であっても、ランダムに初期化されたニューラルネットワークに対して「もっともらしい説明」を与えてしまう現象（Dead Salmon Artifacts）が確認されています。

本記事では、こうした解釈性手法の統計的脆弱性を明らかにします。その上で、解釈性を「統計的・因果的推論」の問題として再定義し、より科学的かつ実用的な検証を行うためのフレームワークと具体的な対策について解説します。

1. AI解釈性が抱える「幻影」と統計的脆弱性

AIの挙動を説明するために開発された多くの手法が、実は「何も学習していないモデル」に対しても、もっともらしい説明を与えてしまうことが明らかになっています。

ランダムなモデルに対する「解釈」

最も衝撃的な事実は、ランダムに重みを初期化しただけのニューラルネットワークに対しても、既存の手法が高精度な「説明」を生成してしまうという点です（Dead Salmon Artifacts）。例えば、重みがランダムなBERTモデルであっても、感情分析タスクにおいて主成分分析やProbing（探索的分類器）を適用すると、驚くべきことに統計的に有意な相関や高い予測精度が観測されてしまう事例が報告されています。

これは、私たちが「モデルが学習した知識」だと思っていたものが、実際にはニューラルネットワークの構造そのものが持つ統計的な偏りや、入力データの特性を見ているに過ぎない可能性を示唆しています。

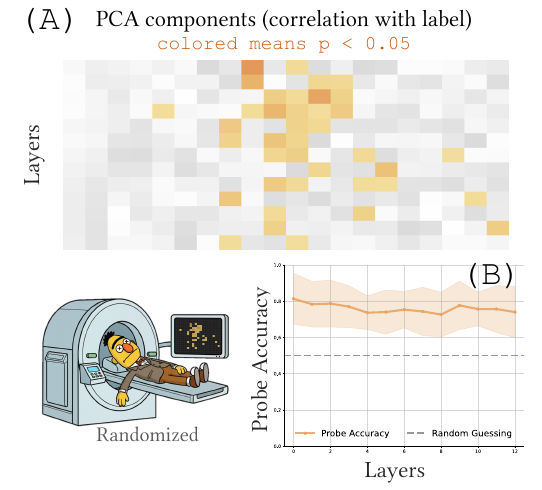
主要な手法における「幻影」の実例

この問題は特定の手法に限った話ではありません。主要な解釈性手法の多くが同様の脆弱性を抱えています。

• Feature Attribution (特徴量寄与): Saliency Mapsなどの勾配ベースの手法において、モデルの重みを完全にランダム化しても、人間にとって視覚的に妥当に見えるヒートマップ（注目領域）が生成され続ける問題が確認されています。
• Probing (プロービング): モデルの中間層から情報を抽出する分類器（プローブ）は、モデルが実際の推論処理には使用していない「死んだ情報」であっても、埋め込み表現に含まれてさえいれば高精度に抽出してしまいます。
• Mechanistic Interpretability (機械的解釈性): 因果関係を特定しようとする回路発見（Circuit Discovery）のような高度な手法であっても、ランダムなネットワークに対して因果的抽象化が成立してしまうケースが報告されています。

共通する原因：統計的識別不能性

重要なのは、これらの失敗が単なるツールのバグや実装ミスではないという点です。根本的な原因は、解釈性というタスクそのものが抱える「統計的識別不能性（Non-identifiability）」にあります。

観測データに対して「もっともらしい説明」が複数成立してしまい、真の因果メカニズムを一意に特定できない状態にあるため、ノイズの中から容易に「存在しないパターン」を見つけ出してしまうのです。

2. なぜ「誤った説明」が生まれるのか：識別不能性と過剰決定

ランダムなモデルから「もっともらしい説明」が得られてしまう現象は、偶然ではありません。これは統計科学における構造的な問題であり、主に「識別不能性」と「過剰決定」という2つの要因に起因しています。

複数の真実が存在する：識別不能性（Non-identifiability）

最も根本的な問題は、観測された計算プロセスに対して、複数の異なる「説明」が等しく適合してしまう状態、「識別不能性」にあります。

機械学習モデルの挙動を説明する際、限られたデータからモデル内部の法則を推定しようとします。しかし、モデルの仕様は不完全であることが多く、データに対して「真の因果メカニズム」も「偶然データに適合しただけの誤った説明」も、同じように成立してしまいます。その結果、解析ツールはノイズの中から、たまたま辻褄が合う説明を選び取ってしまうのです。

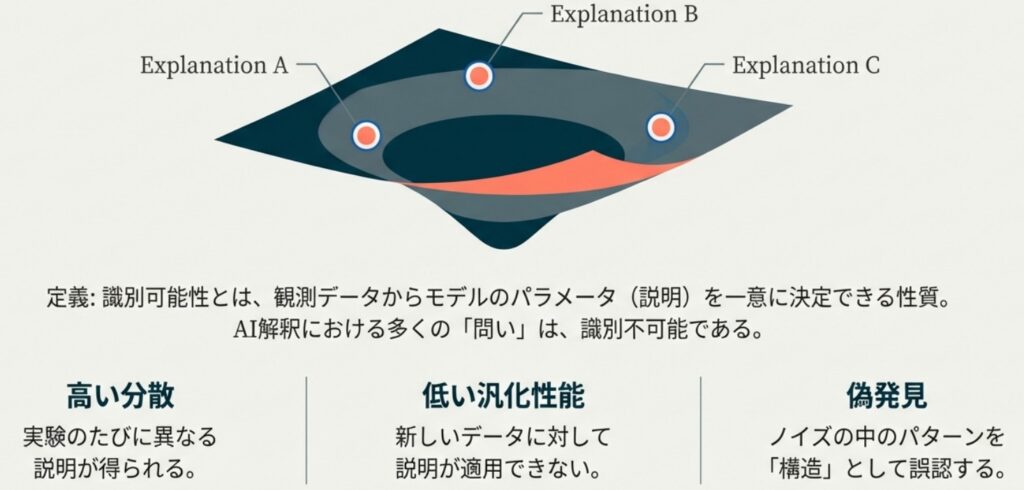
原因を分離できない：因果的過剰決定とヒドラ効果

大規模なニューラルネットワーク特有の「因果的過剰決定（Causal Overdetermination）」も、正確な解釈を妨げる要因です。

モデル内部には、ある機能を実現するために十分なメカニズムが複数、冗長に存在することがあります。これは「ヒドラ効果（Hydra Effect）」とも呼ばれ、ある特定の回路（ニューロンや経路）を遮断しても、別の並列経路が機能して出力が変わらない現象を指します,。結果として、特定の経路を「原因」として分離・特定することが極めて困難になります。

不確実性の欠如が「誤診」を招く

最大の問題は、多くの解釈性手法が結果に対する「確信度（信頼区間）」を提示しない点にあります。

本来、識別不能で過剰決定された状況では、推定の不確実性は非常に大きくなるはずです。しかし、既存の手法はしばしば「点推定（ただ一つの答え）」のみを出力します。これにより、実務者は「たまたま発見されただけの不安定なパターン」を、確固たる真実であると誤認してしまうのです。

3. 解釈性を「統計的・因果的推論」として再定義する

「幻影」に惑わされないためには、解釈性に対するメンタルモデルを転換する必要があります。私たちはしばしば、AIモデルの中に唯一無二の「真の意味」が隠されていると考えがちです。しかし、より科学的で実用的なアプローチは、解釈を「サロゲートモデル（代替モデル）」の推定プロセスとして捉え直すことです。

ここでは、説明を絶対的な真理としてではなく、複雑なAIモデルの挙動を近似するためにデータから推定された「パラメータ」として扱います。

解釈タスクを定義する3つの要素

この統計的フレームワークにおいて、あらゆる解釈性手法は以下の3つの要素で定義されます,。

1. 因果的クエリ（Query Space, $\mu$）: 「何を説明したいか」を定義します。例えば、「特定のニューロンを遮断した場合、出力分布はどう変化するか？」といった介入や反事実的な問いの集合です。
2. 仮説空間（Surrogate Class, $\mathcal{E}$）: 「どのような形式の説明を許容するか」を定義します。線形プローブ、スパースな回路（Circuit）、決定木など、人間が理解可能なモデルの形式を指します。
3. 誤差尺度（Discrepancy Measure, $D$）: 「説明の良さをどう測るか」を定義します。サロゲートモデルによる予測と、実際のAIモデルの挙動（Trace）との間のズレ（例：KL情報量など）を定量化します。

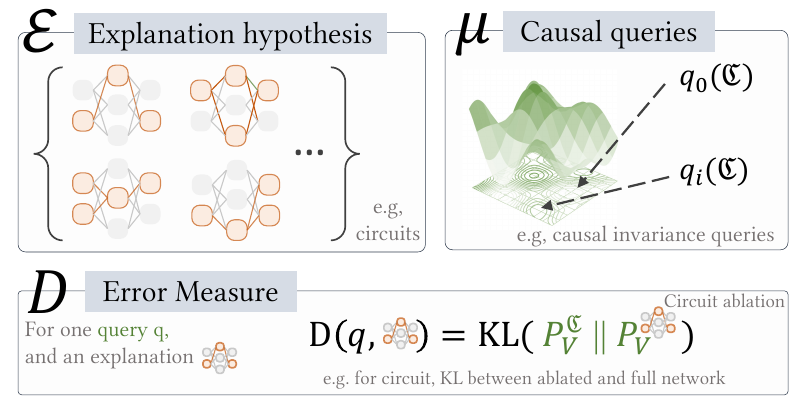
推論としての評価と不確実性

解釈を「統計的推論」として再定義することで、私たちは単なる「もっともらしさ」を超えた評価が可能になります。従来の手法は、たった一つの説明を提示する傾向がありましたが、統計的推論であれば、その説明の偏り（バイアス）や分散（バリアンス）を議論できます。

つまり、「この説明は偶然得られたものではないか？」「データが変われば説明も大きく変わるのではないか？」という不確実性を定量化し、信頼区間を設けることが、信頼できる解釈への第一歩となるのです。

4. 実践的対策：ランダム化ベースの仮説検定

「死んだ鮭」のような誤検出を防ぐ最も確実な方法は、発見されたパターンが「学習の結果」なのか、それとも「アーキテクチャ固有の特性」なのかを区別することです。そのためには、ランダムに初期化されたネットワーク（帰無仮説）をベースラインとして設定する必要があります。

偶然の産物を排除する：具体的な検証手順

従来の手法では、ランダムな推測（チャンスレベル）と比較して精度が高ければ「解釈できた」とみなす傾向がありました。しかし、より厳密な検証を行うには、学習済みモデルで計測したスコア（プローブの正解率や回路の忠実度など）を、ランダムな重みを持つ複数のモデル群から得られるスコア分布と比較します。 モンテカルロ法などを用いてp値を算出し、「偶然では起こり得ない差（統計的有意差）」があるかを検定することで、解釈の信頼性を担保できます。

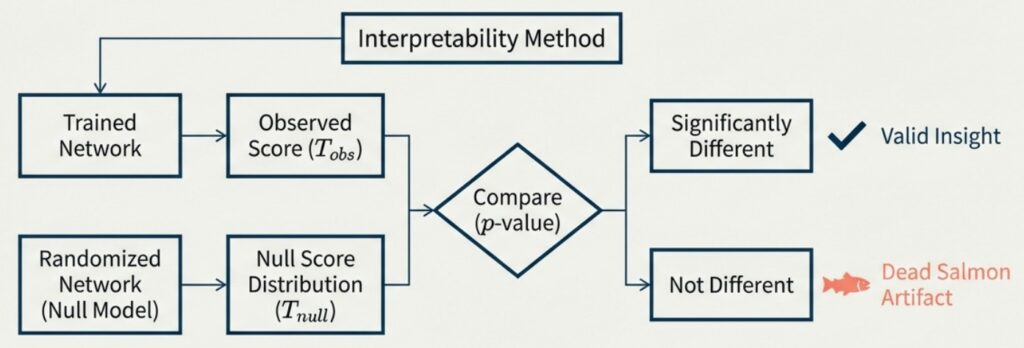
ケーススタディ：検証が暴く「真実」と「偽陽性」

実際にこの「ランダム化テスト」を適用すると、既存の常識を覆す結果が得られています。

• 感情分析 (BERT): 従来の解釈では「感情をコードしている」とされた層も、ランダムモデルと比較すると統計的な有意差が見られず、これまでの発見が偽陽性であった可能性が示唆されました。
• 品詞タグ付け (BERT): 多くの層でランダムモデルとの差は縮小しましたが、中間層においては有意な構造が残存しており、モデルが実際に文法知識を獲得していることが裏付けられました。
• 空間表現 (Pythia): 地理座標を予測するタスクでは、学習済みモデルがランダムモデルを有意に上回るスコアを記録し、モデルが空間概念を正しく学習していることが確認されました。

このように、単に「精度が高い」ことと「メカニズムを解明した」ことは同義ではありません。ランダム化テストは、私たちが手にした説明が「幻影」でないかを確かめるための、強力なリトマス試験紙となるのです。

おわりに

AIの解釈性手法は、かつて神経科学が経験したような統計的な危うさを抱えています。私たちはしばしば、算出されたスコアや美しい可視化結果を「モデルの理解」として受け入れがちですが、それが実はランダムなノイズ由来ではないことを、統計的に検証しなければなりません。

解釈性を実用的な科学にするために必要なのは、不確実性の定量化や、対立仮説（ランダムモデルなど）との比較を標準的なプロセスとして組み込むことです。ツールが提示する結果に対して実務者が抱く「健全な懐疑心」と「厳密な検証」こそが、単なる「もっともらしい説明」を、システム改善に役立つ「信頼できる工学的知見」へと昇華させる鍵となります。

More Information

• arXiv:2512.18792, Maxime Méloux, Giada Dirupo, François Portet, Maxime Peyrard, 「The Dead Salmons of AI Interpretability」, https://www.arxiv.org/abs/2512.18792