近年、深層学習は画像認識などで圧倒的な性能を示していますが、信号処理や画像再構成などの逆問題において、その推論過程が不透明（ブラックボックス）である点が実務的な課題となっています,。特に信頼性が重視されるミッションクリティカルな領域では、AIが「なぜその結果を出したのか」を説明できる解釈性が不可欠です。

この課題を解決するアプローチが、従来の「モデルベースの反復最適化手法」の解釈性と、深層学習の「データ駆動型」の高効率性を融合させる Deep Unfolding（深層展開） です。この技術は、最適化アルゴリズムの各反復ステップをニューラルネットワークの「層」として展開し、内部のパラメータを学習データから最適化します。

これにより、従来の最適化手法よりも遥かに少ない計算ステップ（低遅延）で、モデルの解釈性を保ちつつ、高い推論性能を実現することが可能になります。今回は、Deep Unfoldingの数理的背景から PyTorch を用いた実装、そして様々な発展的テーマまでを詳しく解説します。

1. Deep Unfoldingとは何か？

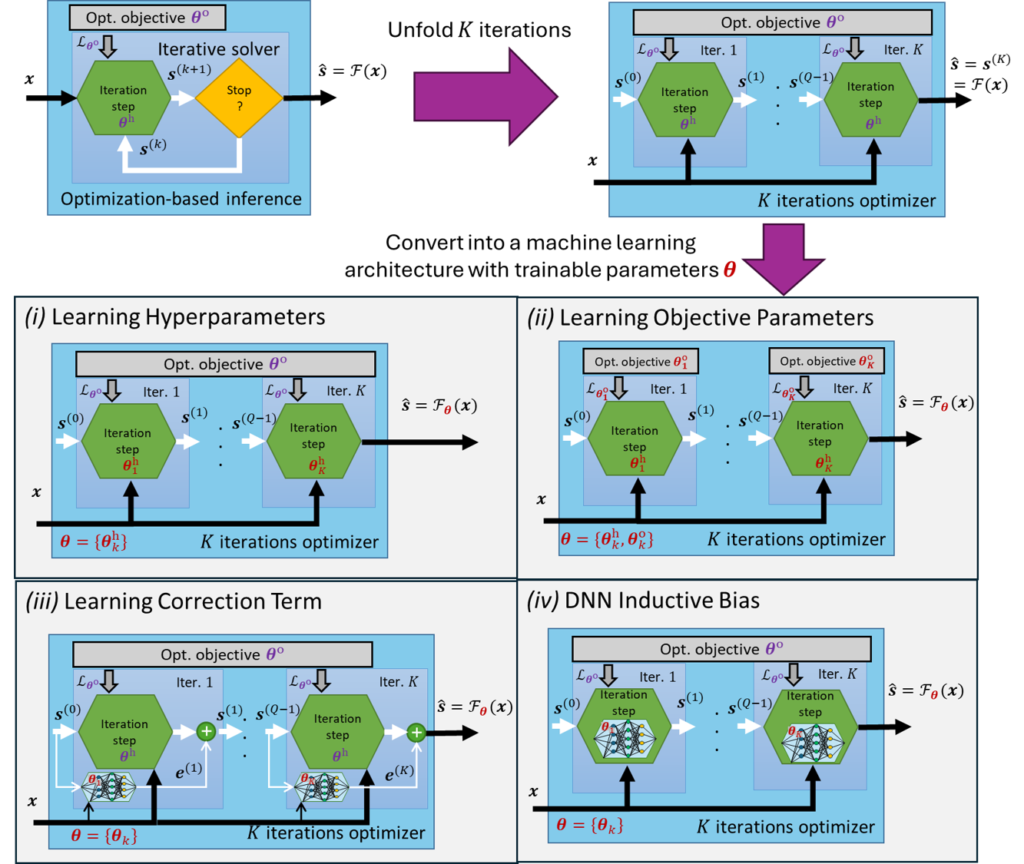
Deep Unfoldingの最大の強みは、その設計が単なるヒューリスティックな試行錯誤ではなく、強固な数理最適化理論に基づいている点にあります。

その根本的な仕組みは、反復最適化アルゴリズムの各イテレーション（反復）をニューラルネットワークの1つの「学習可能な層」として再定義し、それらを有限の深さで連結することです。この構造によって、ネットワークは単なるデータ処理の写像として機能するだけでなく、「特定のデータに適応するために最適化された反復アルゴリズム」として解釈できるようになります。 従来の反復法では、最適な解 \(x^*\) に収束するまでに数100から数1000回の反復計算が必要でしたが、Deep Unfoldingは学習を通じてこのプロセスを劇的に短縮します。

1.1 アルゴリズム展開のメカニズム (ISTA → LISTA)

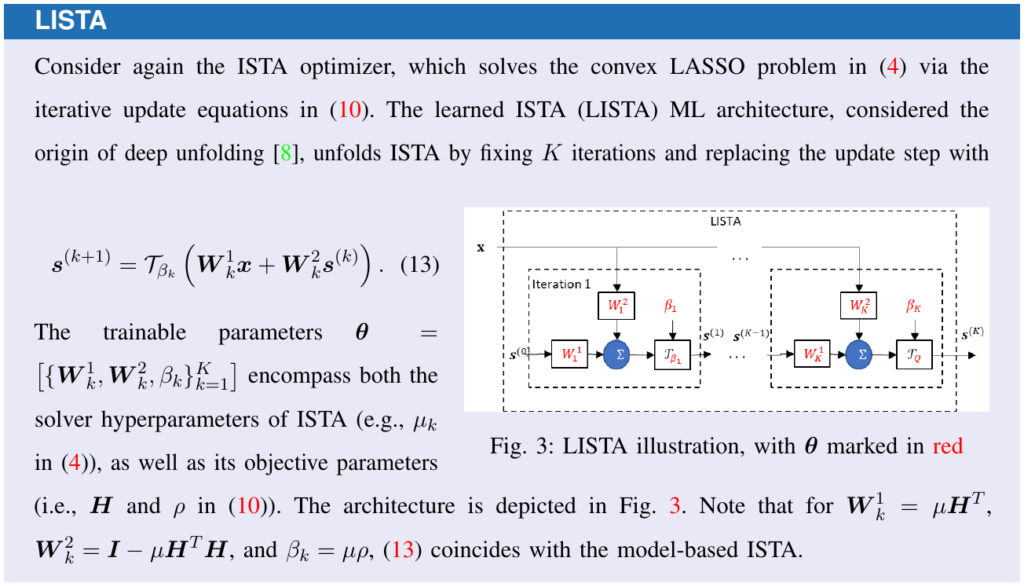
Deep Unfoldingの具体的なイメージを掴むための代表例が、スパース信号復元（LASSO）に用いられる ISTA（Iterative Shrinkage-Thresholding Algorithm：反復収縮閾値アルゴリズム） の展開（Unfolding）です。

ISTAの更新式は、主に以下の2つの解析的な操作から構成されています:

• 勾配降下ステップ： 観測データとの矛盾を減らす操作。
• 近接写像（ソフト閾値操作）： 信号のスパース性を強制する非線形操作。

Deep Unfoldingでは、この更新式に含まれる重み行列（例：\(A^T\) や \(I – \frac{1}{L}A^T A\)）やステップサイズ \(\mu\) を、層ごとに独立した学習可能なパラメータへと置き換えます。 パラメータをデータから学習することで、元のISTAでは膨大な計算が必要だった処理を、例えばわずか10層程度の少ない層数で同等の近似解を得ることが可能になります。こうして誕生した、リカレントニューラルネットワーク（RNN）に似た構造を持つモデルが、Deep Unfoldingの起源とされる LISTA（Learned ISTA） です。

1.2 なぜブラックボックスAIを超えるのか

Deep Unfoldingは、一般的な深層学習モデルが抱える「中身が見えない」という課題に対し、以下の様々な利点を提供します。

• 解釈性 (Interpretability): ネットワークの各層が「データの整合性を高める」「スパース化を適用する」といった明確な数学的ステップに対応しているため、なぜその結果が得られたかを論理的に説明できます。
• 効率性と低遅延: 最適化プロセスを学習フェーズで「最適ルート」に調整するため、推論時の実行時間が大幅に短縮され、リアルタイムアプリケーションに適しています。
• パラメータ効率: 信号の構造に関するドメイン知識をネットワーク自体に組み込んでいるため、ゼロから学習する汎用的なDNNと比較して、学習すべきパラメータの総量が非常に少なくなります。
• 高い汎化性能: 強力な帰納バイアス（構造的な制約）を持つため過学習のリスクが低く、特に訓練データが限定的な医療画像や計測データといったシナリオで、高い性能を発揮します。

2. PyTorchによる実装

Deep Unfoldingの理論を具体化するために、PyTorchを用いた実装例を紹介します。ここでは、信号処理における古典的なアルゴリズム「ISTA」を深層展開（Unfold）した LISTA (Learned ISTA) を構築し、ノイズに埋もれたスパースなパルス信号を復元するタスクに取り組みます。

2.1 信号の選別：ソフト閾値関数

まず、アルゴリズムの核となる「近接写像（Proximal Mapping）」を実装します。

この関数は、入力から一定の強度（閾値：theta）以下の成分をノイズとして除去し、重要な信号成分だけを残す役割を担います。Deep Unfoldingでは、この閾値自体もデータから最適な値を学習します。

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt


# 1. ソフトしきい値関数（信号の選別フィルタ）
# 「一定の強さ（theta）以下のノイズを0にし、それ以上の信号だけを残す」という
# パルス抽出において最も重要な「選別」の役割を担います。
def soft_threshold(x, theta):
    # thetaより小さい値は消去（スパースにする核心部分）
    return torch.sign(x) * torch.relu(torch.abs(x) - theta)

2.2 反復ステップの「層」への変換

次に、ISTAの1回分の反復計算を、ニューラルネットワークの1つの「層」として定義します。

本来のISTAでは物理モデルに基づき固定されていた行列を、学習可能なパラメータ（nn.Parameter）に置き換えるのがDeep Unfoldingの鍵です。これにより、アルゴリズムは様々なデータパターンに適応した「最短の復元ルート」を獲得できるようになります,。

# 2. LISTAの1レイヤー（「観測データの解析」の1ステップ）
class LISTALayer(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(LISTALayer, self).__init__()
        # W1: 観測データ(b)から「信号の種」を見つけ出すための重み
        self.W1 = nn.Parameter(torch.randn(output_dim, input_dim) * 0.1)

        # W2: 前のステップの予測(x)から「不要な干渉」を取り除くための重み
        self.W2 = nn.Parameter(torch.randn(output_dim, output_dim) * 0.1)

        # theta: どの程度の強さを「ノイズ」と見なすかのしきい値（これもデータから学習）
        self.theta = nn.Parameter(torch.ones(output_dim) * 0.01)

    def forward(self, b, x_prev):
        # 観測データからの情報抽出 + 過去の推定値の修正
        z = torch.matmul(b, self.W1.t()) + torch.matmul(x_prev, self.W2.t())

        # 選別フィルタを通して、より「本物らしい」パルスだけを抽出
        return soft_threshold(z, self.theta)

2.3 ネットワークの展開（Unfolding）

定義した層を必要な回数だけスタックし、アルゴリズム全体を「展開」したネットワークを構築します。

nn.ModuleList を使用して反復構造を連結することで、数理アルゴリズムの再帰構造が有限の深さを持つ多層ネットワークへと変換されます。なお、PyTorchの torch.nn.Unfold は画像のパッチ切り出し用関数であり、アルゴリズム展開とは無関係である点に注意が必要です。

# 3. LISTAネットワーク全体（「数理アルゴリズム」を「深層学習」に展開したもの）
class LISTANet(nn.Module):
    def __init__(self, input_dim, output_dim, num_layers=5):
        super(LISTANet, self).__init__()
        # 5回の試行錯誤（5層）で真のパルスを追い求める構造
        self.layers = nn.ModuleList([LISTALayer(input_dim, output_dim) for _ in range(num_layers)])
        self.output_dim = output_dim

    def forward(self, b):
        batch_size = b.size(0)
        # 初期状態は「何も見つかっていない（ゼロ）」からスタート
        x = torch.zeros(batch_size, self.output_dim).to(b.device)
        
        # アルゴリズムを「展開（Unfold）」し、層を重ねるごとに推定精度を高める
        for layer in self.layers:
            x = layer(b, x)
        return x

2.4 逆問題の設定とデータの準備

天体観測などにおいて、装置の制約で不完全な観測データから真の信号を当てる「逆問題（Inverse Problem）」の状況をシミュレートします。

観測データの次元 \(M\) が元の信号 \(N\) より少ない「劣決定系」という困難な課題を、Deep Unfoldingの学習能力で解決する準備を進めます。

# --- 天文学的なシミュレーションデータの作成 ---

# パルス信号の次元(N=100)、観測装置の制約(M=50)
N, M = 100, 50 

# 【真のデータ】数時間の観測の中で、たった数回だけ発生した「真のパルス信号」
# (ほとんどが0であるスパースな状態)
x_true = torch.zeros(N)
x_true[torch.randint(0, N, (5,))] = torch.randn(5) 

# 【物理モデル】天体が発した信号が、観測装置を通る際の「ボケ」や「混合」を表現
A = torch.randn(M, N) 

# 【観測データ】装置の特性(A)を通った信号に、激しい「背景放射ノイズ」が乗ったもの
# (一見するとパルスの位置が全くわからない「密」な状態)
b = torch.matmul(x_true, A.t()) + torch.randn(M) * 0.05 

2.5 学習：アルゴリズムの自己最適化

最後に、一般的な深層学習と同様の手順で、アルゴリズムの内部パラメータを最適化します。

この「教師あり学習」によって、わずか5層程度の極めて浅いネットワークでありながら、従来の反復法を大幅に上回る収束スピードと精度を実現します。これは、最適化アルゴリズムをデータ駆動で「再設計」していることに他なりません。

# --- 学習プロセス ---
model = LISTANet(input_dim=M, output_dim=N, num_layers=5)
optimizer = optim.Adam(model.parameters(), lr=0.01)
criterion = nn.MSELoss()

for epoch in range(200):
    optimizer.zero_grad()
    output = model(b.unsqueeze(0)) # 現在のアルゴリズムで推定
    loss = criterion(output, x_true.unsqueeze(0)) # 真の値とのズレを計算
    loss.backward() # 誤差逆伝播
    optimizer.step() # パラメータ（重みと閾値）を更新

# --- 結果の確認 ---
predicted = model(b.unsqueeze(0)).detach().numpy().flatten()
plt.figure(figsize=(10, 4))
plt.stem(x_true.numpy(), linefmt='g-', markerfmt='go', label='True Pulses (本物の信号)')
plt.stem(predicted, linefmt='r--', markerfmt='rx', label='Recovered by LISTA (抽出された信号)')
plt.title("Astronomy Analogy: Recovering Sparse Pulses from Noisy Data")
plt.legend()
plt.show()

3. 発展的なテーマ

Deep Unfolding（深層展開）は現在、基礎的な実装から一歩進み、様々な最先端の研究テーマへと進化を遂げています。ここでは、実務への応用や理論的深化において注目されている4つの潮流を紹介します。

3.1 無限層モデル（DEQ/Fixed-Point）

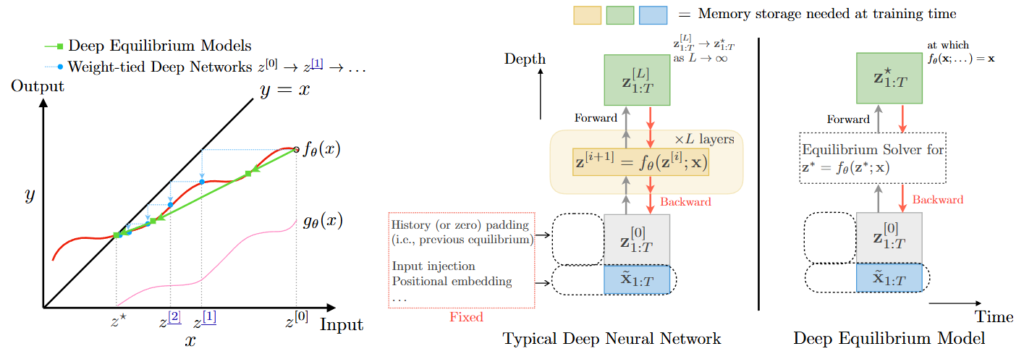
通常の深層展開は有限の層数 \(K\) で計算を打ち切りますが、Deep Equilibrium Models (DEQ) は、ネットワークの全層でパラメータを共有し、反復計算を収束させて得られる「平衡点（Equilibrium Point）」を解として定義するアプローチです。 DEQの最大のメリットはメモリ効率の劇的な向上にあります。陰関数定理（Implicit Function Theorem）を利用することで、通常の深層展開が持つ \(O(K)\) のメモリ消費を \(O(1)\) に削減できるため、特に高次元データに対するメモリ効率の高いスケーラビリティを実現します。

3.2 理論的収束性とALISTA

LISTAの学習パラメータに含まれる冗長性を数学的に解明し、さらに効率化した手法が ALISTA (Analytic LISTA) です。 ALISTAでは、重み行列を相互コヒーレンス（Mutual Coherence）最小化問題の解として事前に計算し、学習時にはステップサイズ \(\mu\) や閾値 \(\theta\) といったスカラーパラメータのみを最適化します。これは、深層展開の本質が「行列の学習」ではなく「アルゴリズムのパス（軌跡）の最適化」にあることを示唆しており、学習コストを最小化する取り組みとして注目されています。

3.3 大域相関とTransformer

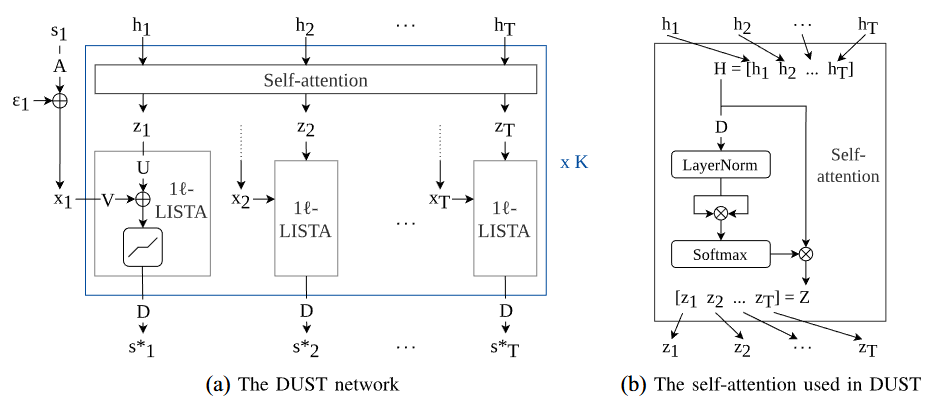
従来のCNNベースの深層展開は局所的な畳み込みに依存していましたが、ビデオや大規模画像の大域的な相関（Long-range dependencies）を捉えるために Transformer のAttention機構を組み込む研究が進んでいます。 例えば DUST (Deep Unfolding Sparse Transformer) では、Attentionの類似度計算をスパースコーディングのプロセスと数理的に結びつけ、物理的な制約を維持しながら大域的な情報を活用するソルバーを構築して精度向上を進めています。

3.4 汎化保証と制約学習

学習データとは異なる分布（OOD: Out-of-Distribution）に対しても高い性能を維持するため、学習プロセスそのものに制約を課す「制約学習」の研究も始まっています。 具体的には、各層の出力が目的関数に対して常に「降下方向」にあるという制約を課すことで、ノイズや分布シフトに対する安定性（ロバスト性）を理論的に保証します。これにより、医療画像や自動運転といった高い信頼性が求められる現場への適用が期待されています。

おわりに

Deep Unfoldingは、数理最適化の厳密な構造と深層学習の柔軟な学習能力を両立する、モデルベース深層学習の中核的な設計パラダイムです。

高い解釈性や計算効率、そして少ない訓練データでの優れた汎化性能という優位性は、特に信頼性が求められるミッションクリティカルな分野や、リソース制約の厳しい環境での応用を強力に推進します。PyTorchのようなモダンなフレームワークを活用すれば、ISTAやADMMなどの最適化理論を基礎としたカスタムネットワークを容易に構築し、様々な実務課題の解決に効率的に取り組むことが可能です。

今後は、スケーラビリティの進化やTransformerの統合による表現力の強化、そして理論的な汎化保証の確立が、この分野のさらなる発展を牽引していくと期待されます。

More Information

• arXiv:2512.03768, Nir Shlezinger et al., 「Deep Unfolding: Recent Developments, Theory, and Design Guidelines」, https://arxiv.org/abs/2512.03768