時系列予測とは、過去の観測データに見られるパターンが将来も継続するという前提に基づき、未来の値を予測する技術です。これは、電力網における需給バランスの維持や、レストランや小売業における在庫の最適化など、ビジネスの様々な場面で不可欠な要素となっています。予測の不確実性が高まる中、単一の数値を予測するだけでなく、確率分布として未来を捉えるアプローチが重要性を増しています。

本記事では、PyTorchやMXNetをバックエンドに採用した、深層学習による確率的時系列モデリングのためのPythonライブラリ「GluonTS」を取り上げます。実務で求められる確率的予測の基礎概念、GluonTSを構成するEstimatorやPredictorといった主要なコンポーネントの設計思想、そしてPythonによる具体的な実装手順について解説します。

1. 確率的時系列予測の基礎

点予測から確率予測へ

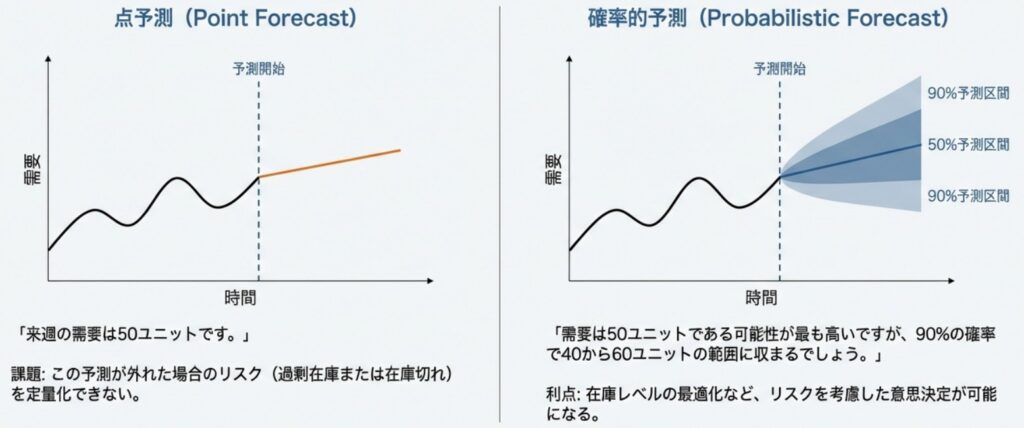
従来の多くの機械学習モデルが行う予測は、未来の特定の時点に対して「単一の値」を返す「点予測（Point Forecast）」が一般的です。しかし、GluonTSが採用するアプローチはこれとは異なります。GluonTSは、将来の値が取り得る「確率分布」を予測します。これは、単に「来月の売上は100万円」と予測するのではなく、「売上が90万円から110万円の間に収まる確率は80%である」といった形で、未来を幅を持って捉えることを意味します。

不確実性の管理

分布を予測することの最大のメリットは、不確実性を定量的に管理できる点にあります。

例えば、レストランで翌日の来店客数を予測するシナリオを考えてみます。「予測値は50人」という一点張りでは、上振れした際の食材不足や、下振れした際の廃棄リスクを評価できません。確率的予測であれば、「中心的な予測は50人だが、60人を超える確率は極めて低い」といった判断が可能になります。これにより、ビジネス上のリスク許容度に応じた、「攻め」や「守り」の在庫戦略を立てることが可能になります。

データの構成要素

GluonTSにおけるデータセットは、主に以下の要素で構成されます。

• ターゲット（Target）: 予測の対象となる時系列データそのものです（例：過去の売上実績や電力消費量）。
• 特徴量（Features）: ターゲットの変動に影響を与える付加情報です。これには大きく分けて2つの種類があります。
  • 動的特徴量（Dynamic Features）: 時間の経過とともに値が変化するものです。例えば、製品の価格、気温、曜日などが該当します。予測を行う未来の期間においても、これらの値が利用可能である必要があります。
  • 静的特徴量（Static Features）: 時間経過によって変化しない属性情報です。店舗ID、商品カテゴリ、設置場所などがこれにあたります。

ユースケース

確率的時系列予測は、特に以下のような領域で重要な役割を果たしています。

• エネルギー需要予測: 電力網において需要と供給のバランスを保つことは極めて重要です。発電事業者は、確率的な需要予測に基づいて供給能力を計画し、過不足のない運用を目指します。
• 在庫・サプライチェーン最適化: 小売業や飲食店において、欠品による機会損失（売り逃し）と、過剰在庫による廃棄コストのバランスを最適化するために利用されます。
• ビジネス・プランニング: 過去のデータパターンが将来も続くと仮定した上で、不確実性を考慮したシナリオ分析を行います。これにより、リスクを許容範囲内に抑えた経営判断が可能になります。

2. GluonTSの設計思想と主要コンポーネント

GluonTSは、時系列予測の実験や本番運用を効率化するために、明確な役割分担を持ったコンポーネント群で構成されています。ここでは、その中心となる設計思想を解説します。

EstimatorとPredictor

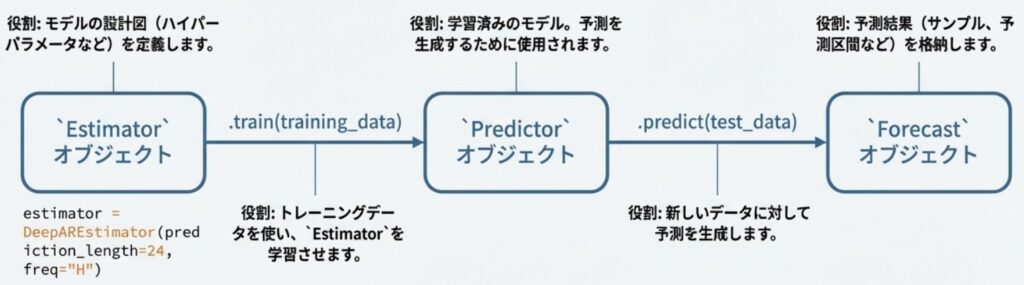
GluonTSにおけるモデルの抽象化は、学習と推論を明確に分離する設計になっています。これを担うのが Estimator と Predictor です。

• Estimator (学習の定義): モデルのネットワーク構造やハイパーパラメータの設定を保持するクラスです。train メソッドに訓練データを渡すことで学習を実行し、その結果として Predictor オブジェクトを生成します。
• Predictor (推論の実行): 学習済みのモデル（パラメータ）を内包したオブジェクトです。predict メソッドを持ち、新しいデータに対して実際に確率的な予測分布を出力します。

この分離により、「学習には時間がかかるが、推論は高速に行いたい」といった実運用のニーズに柔軟に対応できます。

グローバルモデルとローカルモデル

GluonTSの大きな特徴は、データセット全体から一つのモデルを学習するグローバルモデルのサポートです。

• ローカルモデル: ProphetやARIMAのように、単一の時系列データごとにパラメータを適合させる手法です。
• グローバルモデル: DeepARなどの深層学習モデルが該当し、数千〜数万といった多数の時系列データ全体から共通のパターンを学習します。これにより、個々のデータ量が少ない場合でも、類似した系列からの学習情報を活用して高精度な予測が可能になります。

データ処理の仕組み

データパイプラインは、Dataset と Transformation によって構築されます。

• Dataset: データの入れ物です。必須となるのは開始時刻（start）と時系列の値（target）のみで、辞書形式のリストとして扱われます。
• Transformation: データに対する前処理を定義します。例えば、欠損値のフラグ付け、曜日などの時間特徴量の追加、そして学習用に時系列を一定の長さで切り出す処理（InstanceSplitter）などが含まれ、これらを連鎖させることでモデル入力用の形式へ変換します。

3. GluonTSで利用可能なモデル一覧

GluonTSには、最先端の深層学習モデルから古典的な統計モデルのラッパーまで、多種多様なモデルが事前構築済みの状態で提供されています。ユーザーはゼロからネットワークを構築することなく、これらのモデルをインポートするだけですぐに実験を開始できます。

主要なモデルを以下の表にまとめました。これらは主に「グローバルモデル（データセット全体から学習）」と「ローカルモデル（個別の系列ごとに学習）」、そして扱うデータが「単変量（Univariate）」か「多変量（Multivariate）」かによって分類できます。

モデル名	ローカル/グローバル	データ構成	アーキテクチャ / 特徴	実装
DeepAR	グローバル	単変量	RNNを用いた確率的予測の代表的モデル	MXNet, PyTorch
DeepState	グローバル	単変量	RNNと状態空間モデルを組み合わせた手法	MXNet
DeepFactor	グローバル	単変量	RNN、状態空間モデル、ガウス過程を統合	MXNet
Deep Renewal Processes	グローバル	単変量	間欠的な時系列に適したRNNベースのモデル	MXNet
GPForecaster	グローバル	単変量	ガウス過程とMLPを組み合わせた手法	MXNet
MQ-CNN	グローバル	単変量	CNNエンコーダーとMLPデコーダーによる分位点予測	MXNet
MQ-RNN	グローバル	単変量	RNNエンコーダーを用いた分位点予測	MXNet
N-BEATS	グローバル	単変量	残差接続を持つMLPベースの純粋なニューラルネットワーク	MXNet
Rotbaum	グローバル	単変量	LightGBMやXGBoostなどの学習済み木モデルを利用	Numpy
Temporal Fusion Transformer (TFT)	グローバル	単変量	Attention機構とLSTMを組み合わせ、解釈性を重視	MXNet, PyTorch
Transformer	グローバル	単変量	Multi-head attentionを用いたアーキテクチャ	MXNet
WaveNet	グローバル	単変量	拡張因果畳み込み（Dilated convolution）を利用	MXNet, PyTorch
SimpleFeedForward	グローバル	単変量	シンプルな多層パーセプトロン（MLP）	MXNet, PyTorch
MQF2	グローバル	単変量	入力凸ニューラルネットワーク（ICNN）を採用	PyTorch
DeepVAR	グローバル	多変量	多変量時系列に対応したRNNベースのモデル	MXNet
GPVAR	グローバル	多変量	RNNとガウス過程を組み合わせた多変量モデル	MXNet
LSTNet	グローバル	多変量	長期および短期のパターンを捉えるLSTMベースの多変量モデル	MXNet
DeepTPP	グローバル	多変量イベント	時間的点過程（TPP）を用いたイベント予測	MXNet
DeepVARHierarchical	グローバル	階層型	階層的またはグループ化された時系列データの整合性を維持	MXNet
Chronos	グローバル	万能	未学習のデータに対しても予測可能なゼロショット予測モデル群	PyTorch
RForecast	ローカル	単変量	ARIMAやETSなど、R言語の有名なパッケージをラップ	R
Prophet	ローカル	単変量	Facebookが開発した加法的モデルのラップ	Python
NaiveSeasonal	ローカル	単変量	季節性を考慮した単純なベースライン手法	Numpy
NPTS	ローカル	単変量	非媒介的な時系列予測手法	Numpy

モデル選択のポイント

• グローバルモデル vs ローカルモデル: グローバルモデル（DeepARなど）はデータセット全体の多くの時系列から学習するため、トレーニングに時間がかかりますが、似た傾向を持つ複数の系列に対して高い汎用性を持ちます。対してローカルモデル（Prophetなど）は個別の系列ごとに最適化されるため、オンラインでの高速なフィッティングが可能です。
• 確率的予測: GluonTSの多くのモデルは、単一の予測値ではなく分布を予測するため、将来の不確実性を考慮した「予測区間」を算出できるのが大きな特徴です。

GluonTSのモデル群は、「多種多様な道具が揃った専門的なツールボックス」のようなものです。一つのシンプルなモデルであらゆるデータを分析するのではなく、データの複雑さや構造に合わせて最適な道具を選び出せるようになっています。

4. 実装例の紹介

理論や概念の整理ができたところで、実際にPythonコードを用いて動かしてみましょう。ここでは、時系列解析の定番とも言える「AirPassengers（月ごとの飛行機乗客数）」のデータセットを使用し、DeepARモデルで学習から予測までを行う流れを紹介します。

インストール手順

GluonTSは依存関係を最小限に保つ設計になっているため、使用するバックエンド（PyTorchまたはMXNet）に応じて追加のインストールが必要です。今回はPyTorchバックエンドを使用します。

まず、PyTorch環境を整えます（バージョンは環境に合わせて適宜変更してください）。

# まずは、利用したいバージョンのPyTorchを先にインストールしておくことを推奨
$ pip install torch==2.0.0 torchvision==0.15.0 torchaudio==2.0.0

# PyTorchサポートを含むGluonTSをインストール
$ pip install "gluonts[torch]"

# （参考）MXNetを使用したい場合はこちら
# $ pip install "gluonts[mxnet]"

実装のステップ

実装は大きく分けて「データの準備」「データの分割」「モデルの学習」「予測と可視化」の4ステップで進みます。

① ライブラリのインポートとデータの読み込み

まずは必要なライブラリを読み込み、CSVデータをGluonTSが扱えるPandasDataset形式に変換します。

import pandas as pd
import matplotlib.pyplot as plt

from gluonts.dataset.pandas import PandasDataset
from gluonts.dataset.split import split
from gluonts.torch import DeepAREstimator

# Github上のサンプルデータを読み込む
# AirPassengers: 1949年から1960年までの月次乗客数データ
df = pd.read_csv(
    "https://raw.githubusercontent.com/AileenNielsen/"
    "TimeSeriesAnalysisWithPython/master/data/AirPassengers.csv",
    index_col=0,
    parse_dates=True,
)

# DataFrameをGluonTS用のデータセット形式に変換
# target: 予測対象の列名を指定
dataset = PandasDataset(df, target="#Passengers")

➁ 学習用データとテスト用データの分割

時系列データでは、ランダムにデータを間引くのではなく、ある時点を境界として過去と未来に分けるのが一般的です。ここではsplit関数を使用し、データの最後から36ヶ月分（3年分）をテスト用に切り分けます。

# データの分割
# offset=-36: データの末尾36ステップ分をテスト期間として確保し、それ以前を学習データとする
training_data, test_gen = split(dataset, offset=-36)

# テスト用データの生成
# prediction_length: 一度の予測で出力する期間の長さ（ここでは12ヶ月）
# windows: テスト期間からいくつの予測開始点を切り出すか（ここでは3回分）
test_data = test_gen.generate_instances(prediction_length=12, windows=3)

③ モデルの定義と学習

次にEstimator（学習の定義）を設定し、trainメソッドを実行してPredictor（学習済みモデル）を取得します。ここではDeepARモデルを使用します。

# モデルの定義と学習の実行
model = DeepAREstimator(
    prediction_length=12,        # 予測する期間の長さ（12ヶ月）
    freq="M",                    # データの頻度（Month: 月次）
    trainer_kwargs={"max_epochs": 5} # 学習の繰り返し回数（デモ用に少なく設定）
).train(training_data)

④ 予測の実行と可視化

学習済みモデルを使ってテストデータに対する予測を行い、その結果をグラフに描画します。確率的予測であるため、予測結果は一点ではなく分布として出力されます。

# 予測の実行
# test_data.inputを渡すことで、それぞれのウィンドウに対する確率予測が返される
forecasts = list(model.predict(test_data.input))

# 結果の可視化
# 実測値（黒線）をプロット
plt.plot(df["1954":], color="black")

# 予測結果（分布）をプロット
for forecast in forecasts:
    # forecast.plot()は、デフォルトで中央値と予測区間（50%, 90%など）を描画する
    forecast.plot()

plt.legend(["True values"], loc="upper left", fontsize="xx-large")
plt.show()

おわりに

今回は、GluonTSを用いた確率的時系列モデリングについて解説しました。GluonTSを採用する最大の利点は、単一の数値を予測する点予測を超え、確率分布を通じて「未来の不確実性」を可視化できる点にあります。これにより、在庫管理やリソース計画において、リスクを定量的に評価した意思決定が可能になります。また、数千以上の時系列データから共通パターンを学習する「グローバルモデル」のアプローチは、個別のデータ量が少ない場合でも安定した精度を発揮します。

実装面でも、PandasDatasetを利用することでpandasのDataFrameから手軽にデータを投入でき、DeepARをはじめとする豊富なモデル群をすぐに試すことができます。雑なネットワークをスクラッチで実装する必要がなく、実験やビジネス価値の創出に集中できます。

さらに最近では、学習データに含まれない未知の時系列に対しても、ゼロショットで高精度な予測を行う事前学習済みモデル「Chronos」もGluonTSエコシステムから公開されています。進化を続けるGluonTSは、今後の時系列予測のスタンダードとなり得る強力なツールキットです。

More Information

• DeepAR, 「DeepAR: Probabilistic forecasting with autoregressive recurrent networks」, Salinas et al. 2020
• DeepState, 「Deep State Space Models for Time Series Forecasting」, Rangapuram et al. 2018
• DeepFactor, 「Deep Factors for Forecasting」, Wang et al. 2019
• Deep Renewal Processes, 「Forecasting intermittent and sparse time series: A unified probabilistic framework via deep renewal processes」, Türkmen et al. 2021
• MQ-CNN, 「A Multi-Horizon Quantile Recurrent Forecaster」, Wen et al. 2017
• MQ-RNN, 「A Multi-Horizon Quantile Recurrent Forecaster」, Wen et al. 2017
• N-BEATS, 「N-BEATS: Neural basis expansion analysis for interpretable time series forecasting」, Oreshkin et al. 2019
• Rotbaum, 「Probabilistic Forecasting: A Level-Set Approach」, Hasson et al. 2021
• Temporal Fusion Transformer, 「Temporal Fusion Transformers for interpretable multi-horizon time series forecasting」, Lim et al. 2021
• Transformer, 「Attention is All you Need」, Vaswani et al. 2017
• WaveNet, 「WaveNet: A Generative Model for Raw Audio」, van den Oord et al. 2016
• MQF2, 「Multivariate Quantile Function Forecaster」, Kan et al. 2022
• DeepVAR, 「High-dimensional multivariate forecasting with low-rank Gaussian Copula Processes」, Salinas et al. 2019
• GPVAR, 「High-dimensional multivariate forecasting with low-rank Gaussian Copula Processes」, Salinas et al. 2019
• LSTNet, 「Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks」, Lai et al. 2018
• DeepTPP, 「Intensity-Free Learning of Temporal Point Processes」, Oleksandr Shchur et al. 2019
• DeepVARHierarchical, 「End-to-End Learning of Coherent Probabilistic Forecasts for Hierarchical Time Series」, Rangapuram et al. 2021
• RForecast, 「Automatic Time Series Forecasting: The forecast Package for R」, Hyndman et al. 2008
• Prophet, 「Forecasting at Scale」, Taylor et al. 2017
• NaiveSeasonal, 「Seasonal naïve method」, Hyndman et al. 2018